
Question Number 168303 by Mathspace last updated on 07/Apr/22
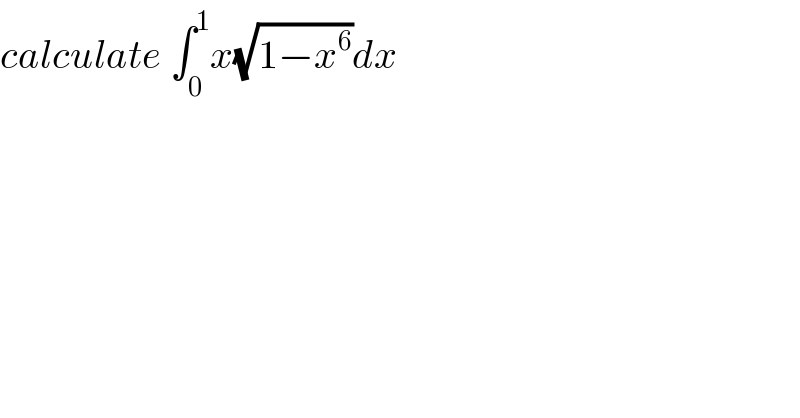
$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}\sqrt{\mathrm{1}−{x}^{\mathrm{6}} }{dx} \\ $$
Answered by peter frank last updated on 07/Apr/22

$$\mathrm{check}\:\mathrm{Qn}\:\mathrm{168231} \\ $$
Answered by Mathspace last updated on 08/Apr/22
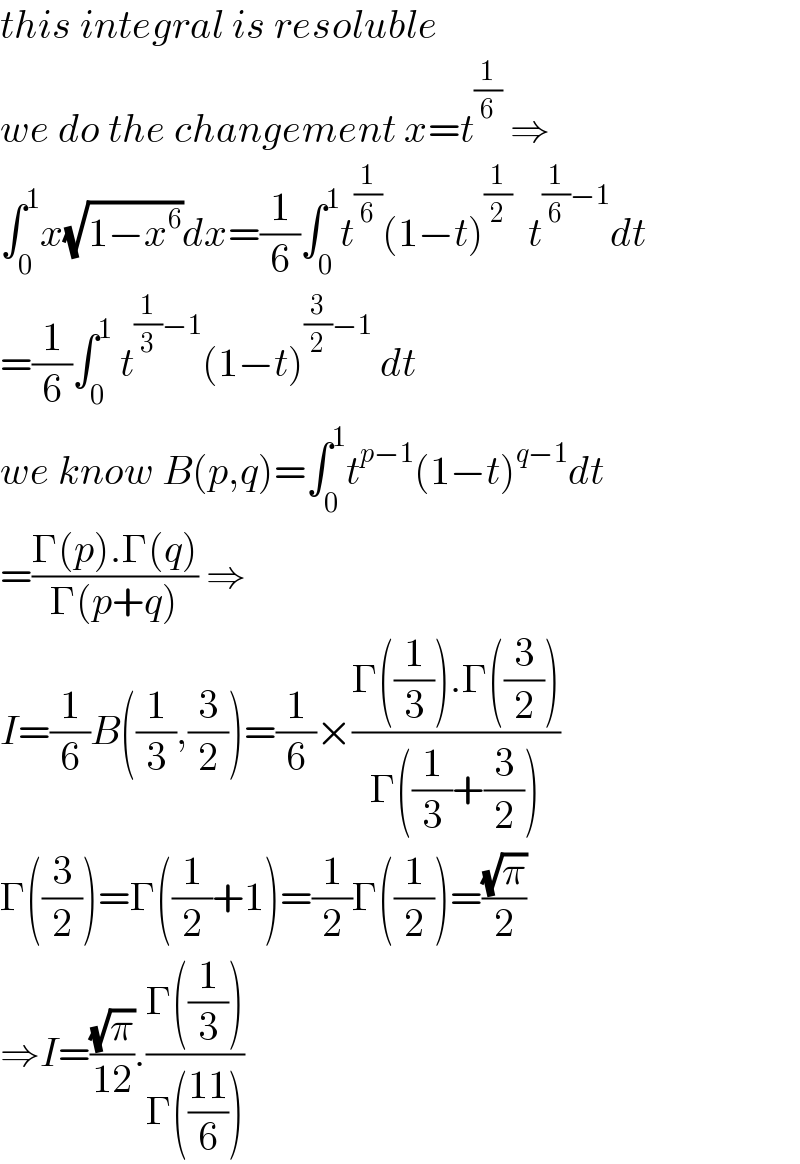
$${this}\:{integral}\:{is}\:{resoluble} \\ $$$${we}\:{do}\:{the}\:{changement}\:{x}={t}^{\frac{\mathrm{1}}{\mathrm{6}}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}\sqrt{\mathrm{1}−{x}^{\mathrm{6}} }{dx}=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\frac{\mathrm{1}}{\mathrm{6}}} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:{t}^{\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} \:{dt} \\ $$$${we}\:{know}\:{B}\left({p},{q}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{p}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{q}−\mathrm{1}} {dt} \\ $$$$=\frac{\Gamma\left({p}\right).\Gamma\left({q}\right)}{\Gamma\left({p}+{q}\right)}\:\Rightarrow \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{6}}{B}\left(\frac{\mathrm{1}}{\mathrm{3}},\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{6}}×\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right).\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$$$\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$\Rightarrow{I}=\frac{\sqrt{\pi}}{\mathrm{12}}.\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)}{\Gamma\left(\frac{\mathrm{11}}{\mathrm{6}}\right)} \\ $$
