
Question Number 168296 by Florian last updated on 07/Apr/22
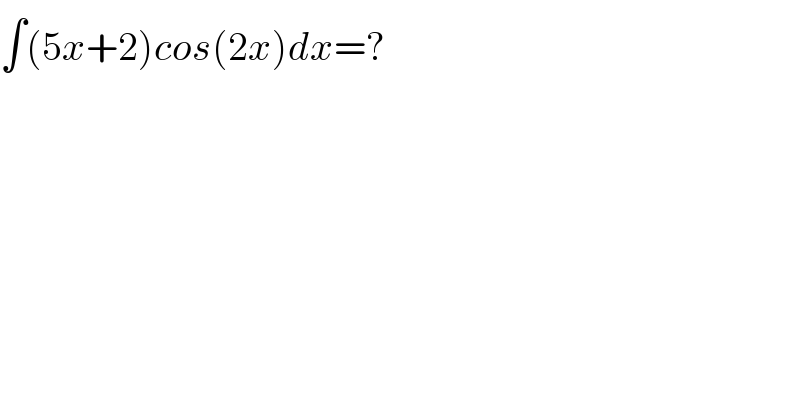
$$\int\left(\mathrm{5}{x}+\mathrm{2}\right){cos}\left(\mathrm{2}{x}\right){dx}=? \\ $$
Answered by floor(10²Eta[1]) last updated on 07/Apr/22
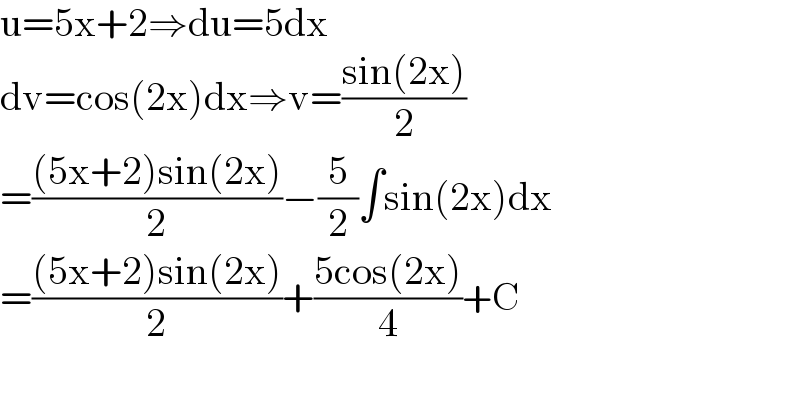
$$\mathrm{u}=\mathrm{5x}+\mathrm{2}\Rightarrow\mathrm{du}=\mathrm{5dx} \\ $$$$\mathrm{dv}=\mathrm{cos}\left(\mathrm{2x}\right)\mathrm{dx}\Rightarrow\mathrm{v}=\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{2}} \\ $$$$=\frac{\left(\mathrm{5x}+\mathrm{2}\right)\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{2}}−\frac{\mathrm{5}}{\mathrm{2}}\int\mathrm{sin}\left(\mathrm{2x}\right)\mathrm{dx} \\ $$$$=\frac{\left(\mathrm{5x}+\mathrm{2}\right)\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{2}}+\frac{\mathrm{5cos}\left(\mathrm{2x}\right)}{\mathrm{4}}+\mathrm{C} \\ $$$$ \\ $$
Commented by Florian last updated on 08/Apr/22

$${Correct}! \\ $$
Answered by peter frank last updated on 07/Apr/22
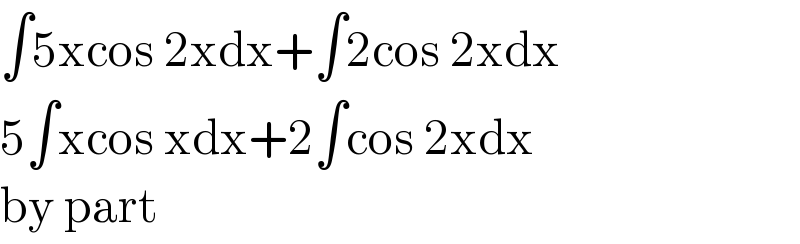
$$\int\mathrm{5xcos}\:\mathrm{2xdx}+\int\mathrm{2cos}\:\mathrm{2xdx} \\ $$$$\mathrm{5}\int\mathrm{xcos}\:\mathrm{xdx}+\mathrm{2}\int\mathrm{cos}\:\mathrm{2xdx} \\ $$$$\mathrm{by}\:\mathrm{part}\: \\ $$
