
Question Number 168143 by cortano1 last updated on 04/Apr/22
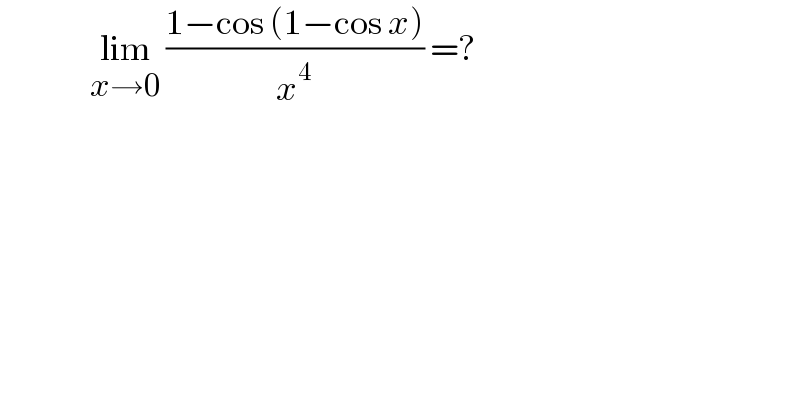
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:\left(\mathrm{1}−\mathrm{cos}\:{x}\right)}{{x}^{\mathrm{4}} }\:=?\:\:\:\:\:\: \\ $$
Answered by qaz last updated on 04/Apr/22
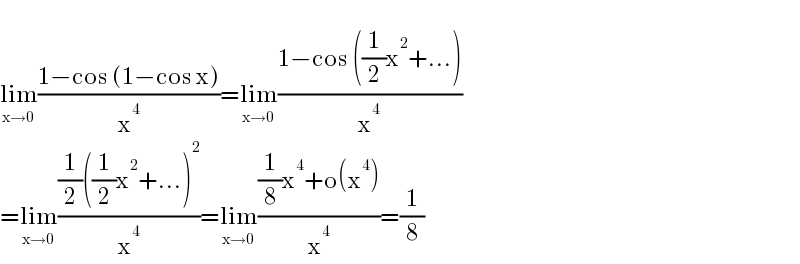
$$ \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:\left(\mathrm{1}−\mathrm{cos}\:\mathrm{x}\right)}{\mathrm{x}^{\mathrm{4}} }=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +...\right)}{\mathrm{x}^{\mathrm{4}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +...\right)^{\mathrm{2}} }{\mathrm{x}^{\mathrm{4}} }=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{8}}\mathrm{x}^{\mathrm{4}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{4}} \right)}{\mathrm{x}^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{8}} \\ $$
Answered by Mathspace last updated on 04/Apr/22
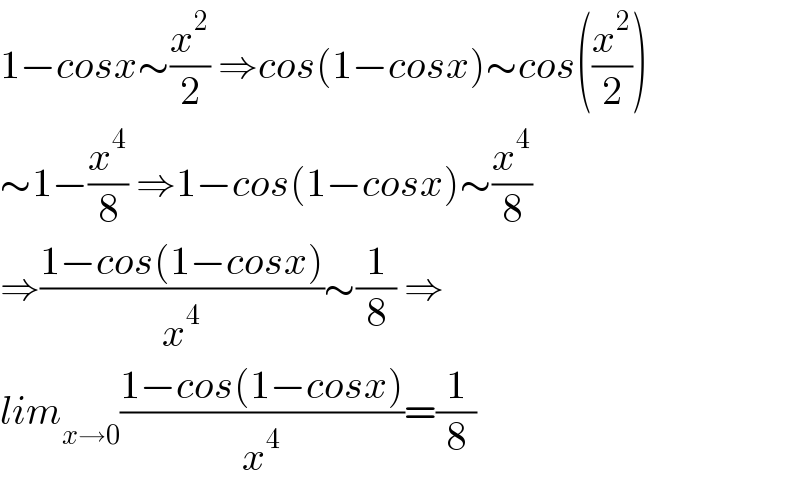
$$\mathrm{1}−{cosx}\sim\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow{cos}\left(\mathrm{1}−{cosx}\right)\sim{cos}\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$\sim\mathrm{1}−\frac{{x}^{\mathrm{4}} }{\mathrm{8}}\:\Rightarrow\mathrm{1}−{cos}\left(\mathrm{1}−{cosx}\right)\sim\frac{{x}^{\mathrm{4}} }{\mathrm{8}} \\ $$$$\Rightarrow\frac{\mathrm{1}−{cos}\left(\mathrm{1}−{cosx}\right)}{{x}^{\mathrm{4}} }\sim\frac{\mathrm{1}}{\mathrm{8}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{1}−{cos}\left(\mathrm{1}−{cosx}\right)}{{x}^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{8}} \\ $$
