
Question Number 168131 by daus last updated on 04/Apr/22
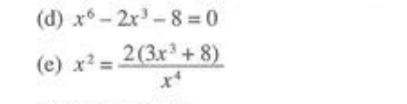
Commented by daus last updated on 04/Apr/22
$${help}\:{me}\:{to}\:{solve}\:{above}\:{equation} \\ $$
Answered by benhamimed last updated on 04/Apr/22
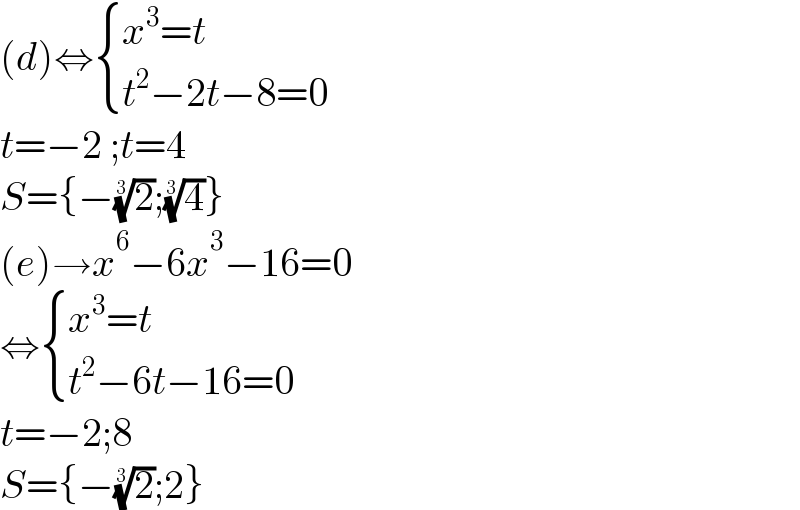
$$\left({d}\right)\Leftrightarrow\begin{cases}{{x}^{\mathrm{3}} ={t}}\\{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{8}=\mathrm{0}}\end{cases} \\ $$$${t}=−\mathrm{2}\:;{t}=\mathrm{4} \\ $$$${S}=\left\{−\sqrt[{\mathrm{3}}]{\mathrm{2}};\sqrt[{\mathrm{3}}]{\mathrm{4}}\right\} \\ $$$$\left({e}\right)\rightarrow{x}^{\mathrm{6}} −\mathrm{6}{x}^{\mathrm{3}} −\mathrm{16}=\mathrm{0} \\ $$$$\Leftrightarrow\begin{cases}{{x}^{\mathrm{3}} ={t}}\\{{t}^{\mathrm{2}} −\mathrm{6}{t}−\mathrm{16}=\mathrm{0}}\end{cases} \\ $$$${t}=−\mathrm{2};\mathrm{8} \\ $$$${S}=\left\{−\sqrt[{\mathrm{3}}]{\mathrm{2}};\mathrm{2}\right\} \\ $$
Answered by MJS_new last updated on 04/Apr/22
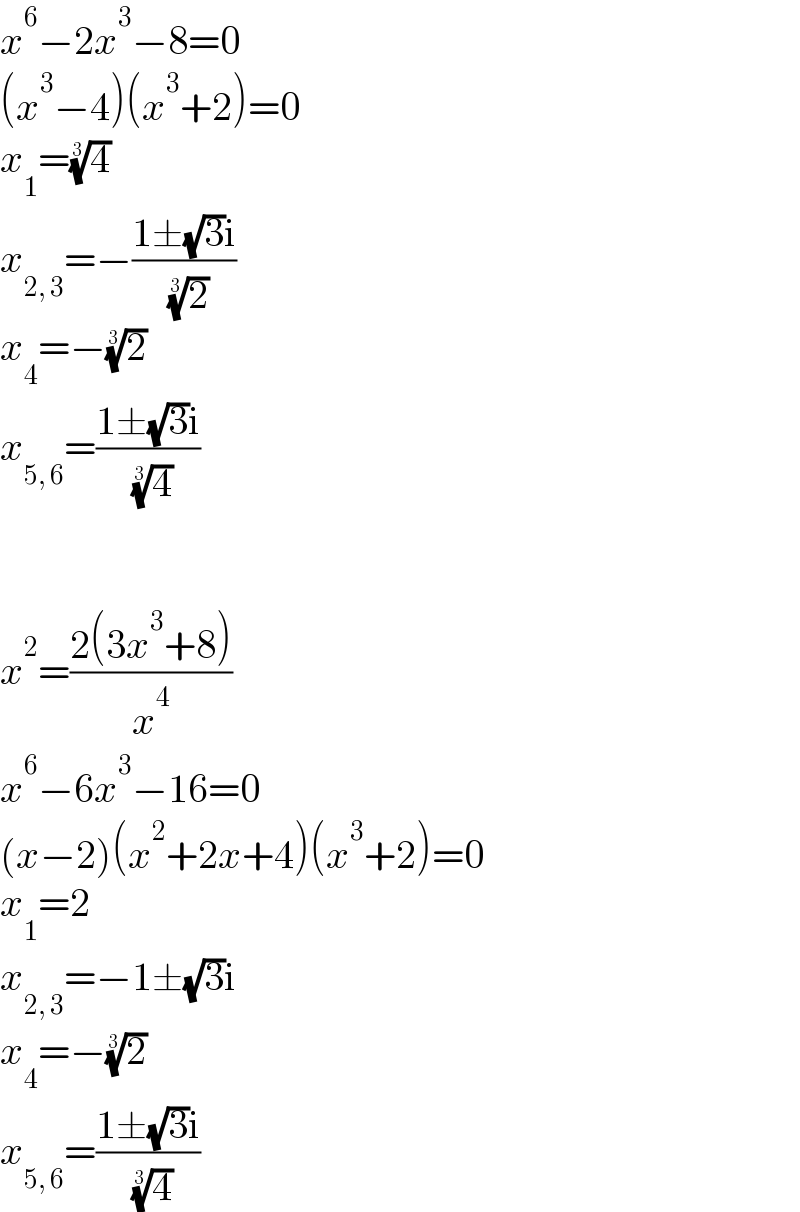
$${x}^{\mathrm{6}} −\mathrm{2}{x}^{\mathrm{3}} −\mathrm{8}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{3}} −\mathrm{4}\right)\left({x}^{\mathrm{3}} +\mathrm{2}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\sqrt[{\mathrm{3}}]{\mathrm{4}} \\ $$$${x}_{\mathrm{2},\:\mathrm{3}} =−\frac{\mathrm{1}\pm\sqrt{\mathrm{3}}\mathrm{i}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}} \\ $$$${x}_{\mathrm{4}} =−\sqrt[{\mathrm{3}}]{\mathrm{2}} \\ $$$${x}_{\mathrm{5},\:\mathrm{6}} =\frac{\mathrm{1}\pm\sqrt{\mathrm{3}}\mathrm{i}}{\:\sqrt[{\mathrm{3}}]{\mathrm{4}}} \\ $$$$ \\ $$$$ \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{2}\left(\mathrm{3}{x}^{\mathrm{3}} +\mathrm{8}\right)}{{x}^{\mathrm{4}} } \\ $$$${x}^{\mathrm{6}} −\mathrm{6}{x}^{\mathrm{3}} −\mathrm{16}=\mathrm{0} \\ $$$$\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)\left({x}^{\mathrm{3}} +\mathrm{2}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{2} \\ $$$${x}_{\mathrm{2},\:\mathrm{3}} =−\mathrm{1}\pm\sqrt{\mathrm{3}}\mathrm{i} \\ $$$${x}_{\mathrm{4}} =−\sqrt[{\mathrm{3}}]{\mathrm{2}} \\ $$$${x}_{\mathrm{5},\:\mathrm{6}} =\frac{\mathrm{1}\pm\sqrt{\mathrm{3}}\mathrm{i}}{\:\sqrt[{\mathrm{3}}]{\mathrm{4}}} \\ $$
