
Question Number 168119 by Beginner last updated on 03/Apr/22

Answered by mr W last updated on 04/Apr/22
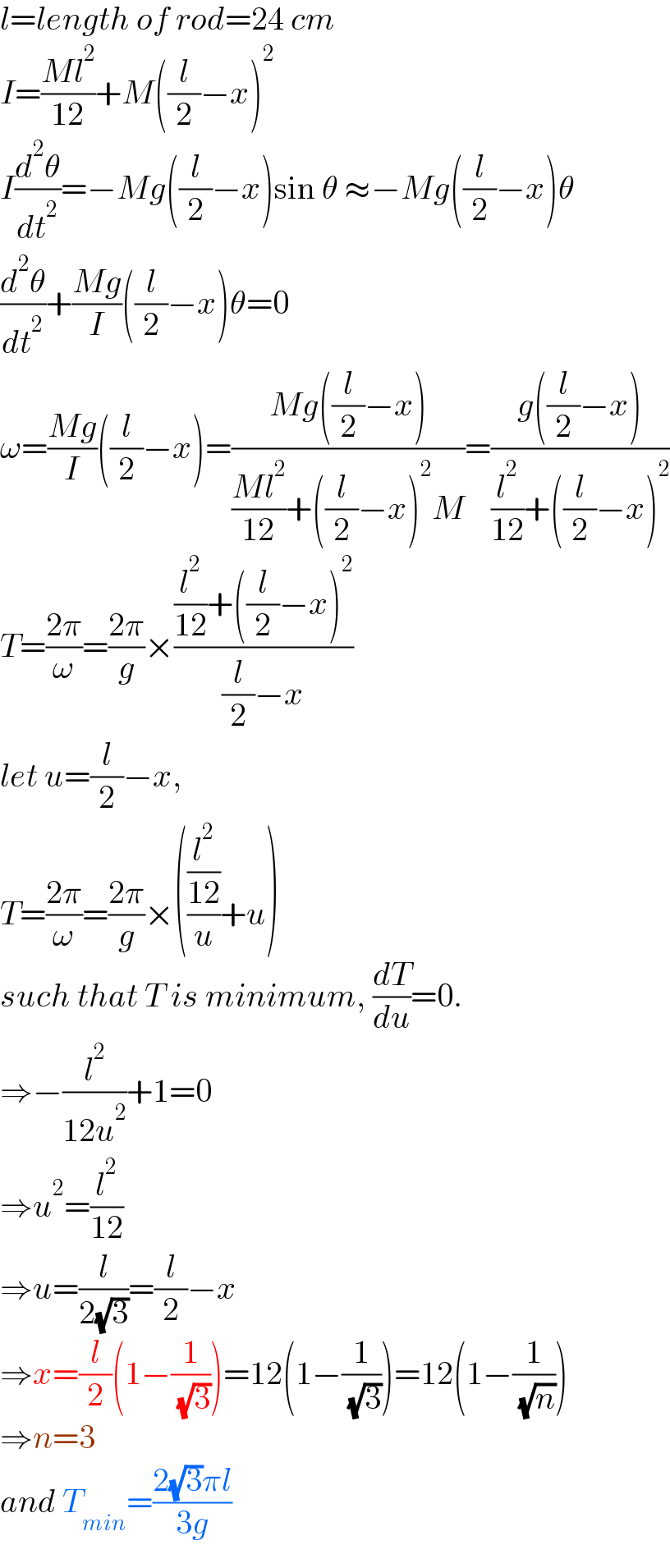
$${l}={length}\:{of}\:{rod}=\mathrm{24}\:{cm} \\ $$$${I}=\frac{{Ml}^{\mathrm{2}} }{\mathrm{12}}+{M}\left(\frac{{l}}{\mathrm{2}}−{x}\right)^{\mathrm{2}} \\ $$$${I}\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }=−{Mg}\left(\frac{{l}}{\mathrm{2}}−{x}\right)\mathrm{sin}\:\theta\:\approx−{Mg}\left(\frac{{l}}{\mathrm{2}}−{x}\right)\theta \\ $$$$\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }+\frac{{Mg}}{{I}}\left(\frac{{l}}{\mathrm{2}}−{x}\right)\theta=\mathrm{0} \\ $$$$\omega=\frac{{Mg}}{{I}}\left(\frac{{l}}{\mathrm{2}}−{x}\right)=\frac{{Mg}\left(\frac{{l}}{\mathrm{2}}−{x}\right)}{\frac{{Ml}^{\mathrm{2}} }{\mathrm{12}}+\left(\frac{{l}}{\mathrm{2}}−{x}\right)^{\mathrm{2}} {M}}=\frac{{g}\left(\frac{{l}}{\mathrm{2}}−{x}\right)}{\frac{{l}^{\mathrm{2}} }{\mathrm{12}}+\left(\frac{{l}}{\mathrm{2}}−{x}\right)^{\mathrm{2}} } \\ $$$${T}=\frac{\mathrm{2}\pi}{\omega}=\frac{\mathrm{2}\pi}{{g}}×\frac{\frac{{l}^{\mathrm{2}} }{\mathrm{12}}+\left(\frac{{l}}{\mathrm{2}}−{x}\right)^{\mathrm{2}} }{\frac{{l}}{\mathrm{2}}−{x}} \\ $$$${let}\:{u}=\frac{{l}}{\mathrm{2}}−{x}, \\ $$$${T}=\frac{\mathrm{2}\pi}{\omega}=\frac{\mathrm{2}\pi}{{g}}×\left(\frac{\frac{{l}^{\mathrm{2}} }{\mathrm{12}}}{{u}}+{u}\right) \\ $$$${such}\:{that}\:{T}\:{is}\:{minimum},\:\frac{{dT}}{{du}}=\mathrm{0}. \\ $$$$\Rightarrow−\frac{{l}^{\mathrm{2}} }{\mathrm{12}{u}^{\mathrm{2}} }+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{u}^{\mathrm{2}} =\frac{{l}^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\Rightarrow{u}=\frac{{l}}{\mathrm{2}\sqrt{\mathrm{3}}}=\frac{{l}}{\mathrm{2}}−{x} \\ $$$$\Rightarrow{x}=\frac{{l}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)=\mathrm{12}\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)=\mathrm{12}\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{{n}}}\right) \\ $$$$\Rightarrow{n}=\mathrm{3} \\ $$$${and}\:{T}_{{min}} =\frac{\mathrm{2}\sqrt{\mathrm{3}}\pi{l}}{\mathrm{3}{g}} \\ $$
Commented by Beginner last updated on 03/Apr/22

$${Thanks} \\ $$
Commented by Tawa11 last updated on 03/Apr/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Commented by peter frank last updated on 04/Apr/22
$$\mathrm{good}\:\mathrm{question}.\mathrm{Rotation}\:\mathrm{dynamics} \\ $$
