Question and Answers Forum

All Question   Topic List

Question Number 168026 by mathlove last updated on 01/Apr/22

$$ \\ $$ Math question for anyone who has a bonus code solution. Question. Find the smallest numbers that are divisible by 15 remain 9 and divide by 25 remain 19 and divide by 18 remain 12 remain and divide by 36 remain 30 remain and divide above 40 remain 34 remain Whoever solves it on the sheet, put his photo in the comment again.\\n

Commented bymr W last updated on 01/Apr/22

1794

$$\mathrm{1794} \\ $$

Answered by mr W last updated on 01/Apr/22

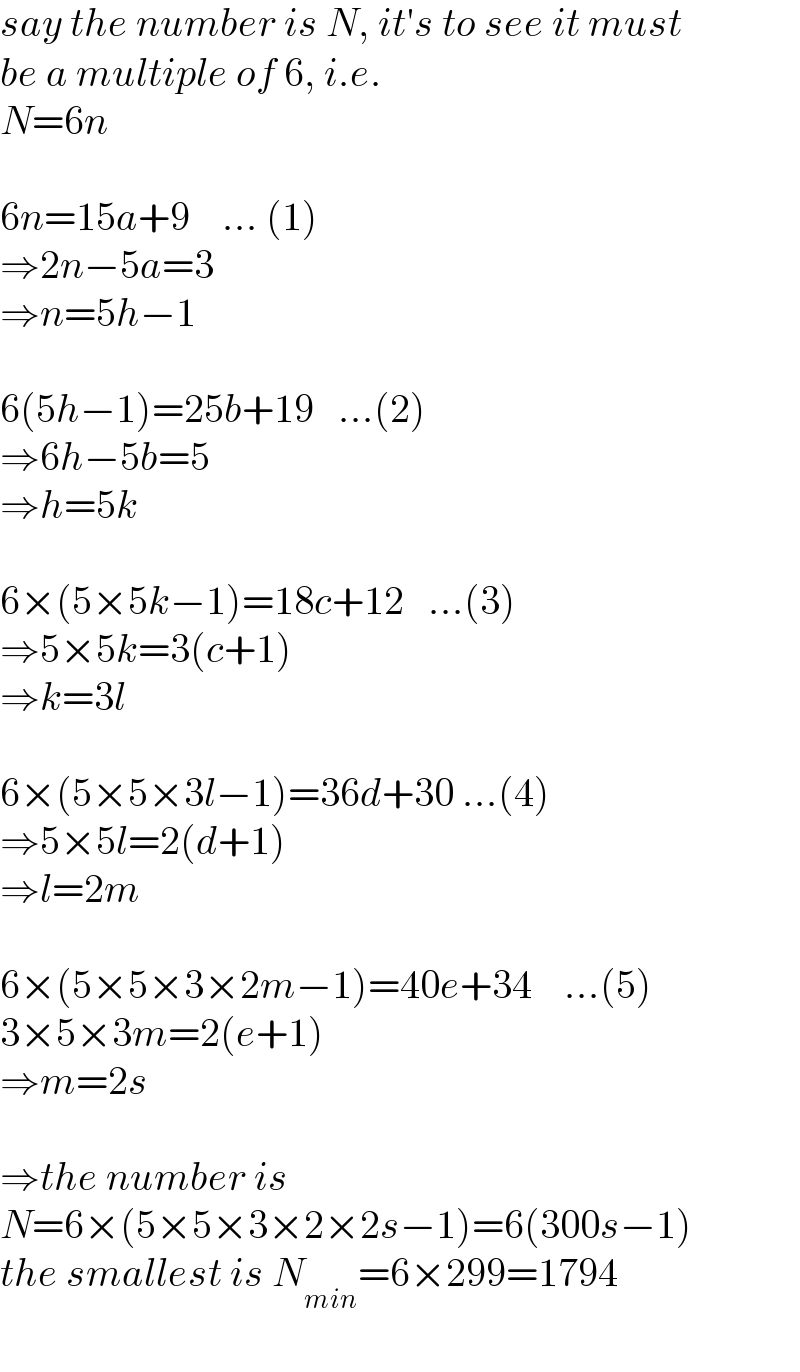
say the number is N, it′s to see it must be a multiple of 6, i.e. N=6n 6n=15a+9 ... (1) ⇒2n−5a=3 ⇒n=5h−1 6(5h−1)=25b+19 ...(2) ⇒6h−5b=5 ⇒h=5k 6×(5×5k−1)=18c+12 ...(3) ⇒5×5k=3(c+1) ⇒k=3l 6×(5×5×3l−1)=36d+30 ...(4) ⇒5×5l=2(d+1) ⇒l=2m 6×(5×5×3×2m−1)=40e+34 ...(5) 3×5×3m=2(e+1) ⇒m=2s ⇒the number is N=6×(5×5×3×2×2s−1)=6(300s−1) the smallest is N_(min) =6×299=1794

$${say}\:{the}\:{number}\:{is}\:{N},\:{it}'{s}\:{to}\:{see}\:{it}\:{must} \\ $$ $${be}\:{a}\:{multiple}\:{of}\:\mathrm{6},\:{i}.{e}. \\ $$ $${N}=\mathrm{6}{n} \\ $$ $$ \\ $$ $$\mathrm{6}{n}=\mathrm{15}{a}+\mathrm{9}\:\:\:\:...\:\left(\mathrm{1}\right) \\ $$ $$\Rightarrow\mathrm{2}{n}−\mathrm{5}{a}=\mathrm{3}\: \\ $$ $$\Rightarrow{n}=\mathrm{5}{h}−\mathrm{1} \\ $$ $$ \\ $$ $$\mathrm{6}\left(\mathrm{5}{h}−\mathrm{1}\right)=\mathrm{25}{b}+\mathrm{19}\:\:\:...\left(\mathrm{2}\right) \\ $$ $$\Rightarrow\mathrm{6}{h}−\mathrm{5}{b}=\mathrm{5} \\ $$ $$\Rightarrow{h}=\mathrm{5}{k} \\ $$ $$ \\ $$ $$\mathrm{6}×\left(\mathrm{5}×\mathrm{5}{k}−\mathrm{1}\right)=\mathrm{18}{c}+\mathrm{12}\:\:\:...\left(\mathrm{3}\right) \\ $$ $$\Rightarrow\mathrm{5}×\mathrm{5}{k}=\mathrm{3}\left({c}+\mathrm{1}\right) \\ $$ $$\Rightarrow{k}=\mathrm{3}{l} \\ $$ $$ \\ $$ $$\mathrm{6}×\left(\mathrm{5}×\mathrm{5}×\mathrm{3}{l}−\mathrm{1}\right)=\mathrm{36}{d}+\mathrm{30}\:...\left(\mathrm{4}\right) \\ $$ $$\Rightarrow\mathrm{5}×\mathrm{5}{l}=\mathrm{2}\left({d}+\mathrm{1}\right) \\ $$ $$\Rightarrow{l}=\mathrm{2}{m} \\ $$ $$ \\ $$ $$\mathrm{6}×\left(\mathrm{5}×\mathrm{5}×\mathrm{3}×\mathrm{2}{m}−\mathrm{1}\right)=\mathrm{40}{e}+\mathrm{34}\:\:\:\:...\left(\mathrm{5}\right) \\ $$ $$\mathrm{3}×\mathrm{5}×\mathrm{3}{m}=\mathrm{2}\left({e}+\mathrm{1}\right) \\ $$ $$\Rightarrow{m}=\mathrm{2}{s} \\ $$ $$ \\ $$ $$\Rightarrow{the}\:{number}\:{is} \\ $$ $${N}=\mathrm{6}×\left(\mathrm{5}×\mathrm{5}×\mathrm{3}×\mathrm{2}×\mathrm{2}{s}−\mathrm{1}\right)=\mathrm{6}\left(\mathrm{300}{s}−\mathrm{1}\right) \\ $$ $${the}\:{smallest}\:{is}\:{N}_{{min}} =\mathrm{6}×\mathrm{299}=\mathrm{1794} \\ $$

Commented bymathlove last updated on 01/Apr/22

thanks mr W

$${thanks}\:{mr}\:{W} \\ $$

Commented byTawa11 last updated on 01/Apr/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com