
Question Number 168013 by leicianocosta last updated on 31/Mar/22

Answered by nurtani last updated on 31/Mar/22
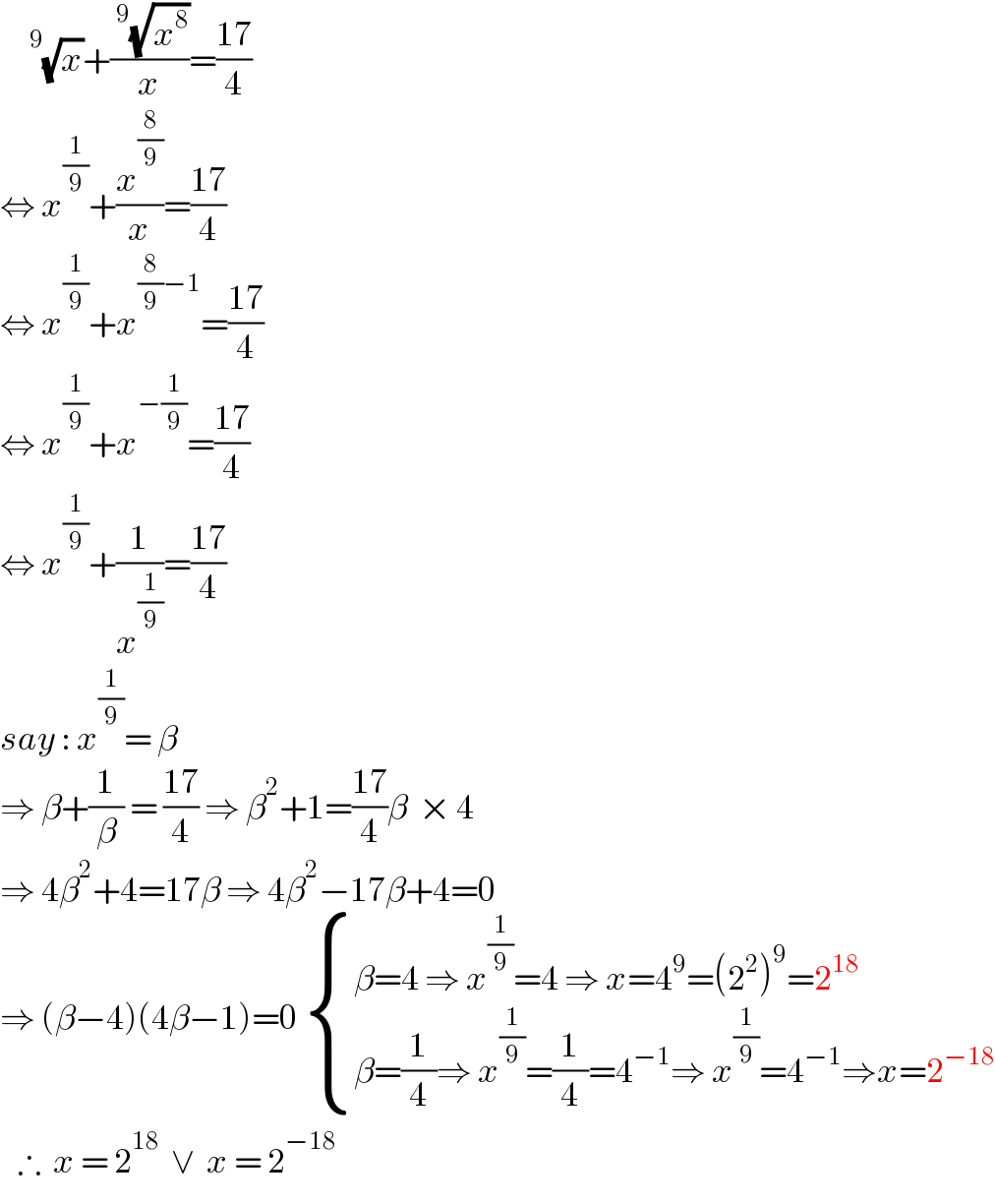
$$\:\:\:\:\:^{\mathrm{9}} \sqrt{{x}}+\frac{\:^{\mathrm{9}} \sqrt{{x}^{\mathrm{8}} }}{{x}}=\frac{\mathrm{17}}{\mathrm{4}} \\ $$$$\Leftrightarrow\:{x}^{\frac{\mathrm{1}}{\mathrm{9}}} +\frac{{x}^{\frac{\mathrm{8}}{\mathrm{9}}} }{{x}}=\frac{\mathrm{17}}{\mathrm{4}} \\ $$$$\Leftrightarrow\:{x}^{\frac{\mathrm{1}}{\mathrm{9}}} +{x}^{\frac{\mathrm{8}}{\mathrm{9}}−\mathrm{1}} =\frac{\mathrm{17}}{\mathrm{4}} \\ $$$$\Leftrightarrow\:{x}^{\frac{\mathrm{1}}{\mathrm{9}}} +{x}^{−\frac{\mathrm{1}}{\mathrm{9}}} =\frac{\mathrm{17}}{\mathrm{4}} \\ $$$$\Leftrightarrow\:{x}^{\frac{\mathrm{1}}{\mathrm{9}}} +\frac{\mathrm{1}}{{x}^{\frac{\mathrm{1}}{\mathrm{9}}} }=\frac{\mathrm{17}}{\mathrm{4}} \\ $$$${say}\::\:{x}^{\frac{\mathrm{1}}{\mathrm{9}}} =\:\beta \\ $$$$\Rightarrow\:\beta+\frac{\mathrm{1}}{\beta}\:=\:\frac{\mathrm{17}}{\mathrm{4}}\:\Rightarrow\:\beta^{\mathrm{2}} +\mathrm{1}=\frac{\mathrm{17}}{\mathrm{4}}\beta\:\:×\:\mathrm{4} \\ $$$$\Rightarrow\:\mathrm{4}\beta^{\mathrm{2}} +\mathrm{4}=\mathrm{17}\beta\:\Rightarrow\:\mathrm{4}\beta^{\mathrm{2}} −\mathrm{17}\beta+\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow\:\left(\beta−\mathrm{4}\right)\left(\mathrm{4}\beta−\mathrm{1}\right)=\mathrm{0}\:\begin{cases}{\beta=\mathrm{4}\:\Rightarrow\:{x}^{\frac{\mathrm{1}}{\mathrm{9}}} =\mathrm{4}\:\Rightarrow\:{x}=\mathrm{4}^{\mathrm{9}} =\left(\mathrm{2}^{\mathrm{2}} \right)^{\mathrm{9}} =\mathrm{2}^{\mathrm{18}} }\\{\beta=\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow\:{x}^{\frac{\mathrm{1}}{\mathrm{9}}} =\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{4}^{−\mathrm{1}} \Rightarrow\:{x}^{\frac{\mathrm{1}}{\mathrm{9}}} =\mathrm{4}^{−\mathrm{1}} \Rightarrow{x}=\mathrm{2}^{−\mathrm{18}} }\end{cases} \\ $$$$\:\:\:\therefore\:\:{x}\:=\:\mathrm{2}^{\mathrm{18}} \:\:\vee\:\:{x}\:=\:\mathrm{2}^{−\mathrm{18}} \\ $$
Answered by yogamulyadi last updated on 01/Apr/22

$$\sqrt[{\mathrm{9}}]{{x}}+\frac{\mathrm{1}}{\:\sqrt[{\mathrm{9}}]{{x}}}=\mathrm{4}+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\sqrt[{\mathrm{9}}]{{x}}=\mathrm{4}^{\pm\mathrm{1}} =\mathrm{2}^{\pm\mathrm{2}} \\ $$$${x}\in\left\{\mathrm{2}^{-\mathrm{18}} ,\:\mathrm{2}^{\mathrm{18}} \right\} \\ $$$$. \\ $$$$. \\ $$$${sorry},\:{not}\:{understand}\:{the}\:{language} \\ $$
