
Question Number 167929 by Huy last updated on 29/Mar/22
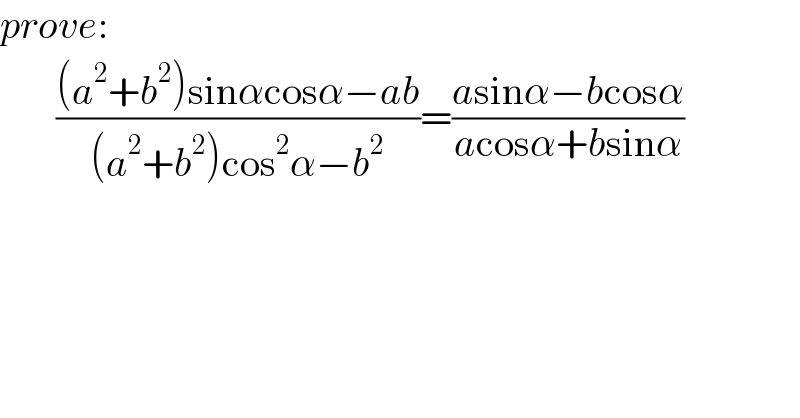
$${prove}:\: \\ $$$$\:\:\:\:\:\:\:\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\mathrm{sin}\alpha\mathrm{cos}\alpha−{ab}}{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \alpha−{b}^{\mathrm{2}} }=\frac{{a}\mathrm{sin}\alpha−{b}\mathrm{cos}\alpha}{{a}\mathrm{cos}\alpha+{b}\mathrm{sin}\alpha} \\ $$
Answered by som(math1967) last updated on 29/Mar/22

$$\frac{{a}^{\mathrm{2}} {sin}\alpha{cos}\alpha+{b}^{\mathrm{2}} {sin}\alpha{cos}\alpha−{absin}^{\mathrm{2}} \alpha−{abcos}^{\mathrm{2}} \alpha}{{a}^{\mathrm{2}} {cos}^{\mathrm{2}} \alpha−{b}^{\mathrm{2}} \left(\mathrm{1}−{cos}^{\mathrm{2}} \alpha\right)} \\ $$$$=\frac{{asin}\alpha\left({acos}\alpha−{bsin}\alpha\right)−{bcos}\alpha\left({acos}\alpha−{bsin}\alpha\right)}{{a}^{\mathrm{2}} {cos}^{\mathrm{2}} \alpha−{b}^{\mathrm{2}} {sin}^{\mathrm{2}} \alpha} \\ $$$$=\frac{\left({acos}\alpha−{bsin}\alpha\right)\left({asin}\alpha−{bcos}\alpha\right)}{\left({acos}\alpha+{bsin}\alpha\right)\left({acos}\alpha−{bsin}\alpha\right)} \\ $$$$=\frac{{asin}\alpha−{bcos}\alpha}{{acos}\alpha+{bsin}\alpha} \\ $$$$\:\:\left({proved}\right) \\ $$
