
Question Number 167922 by peter frank last updated on 29/Mar/22
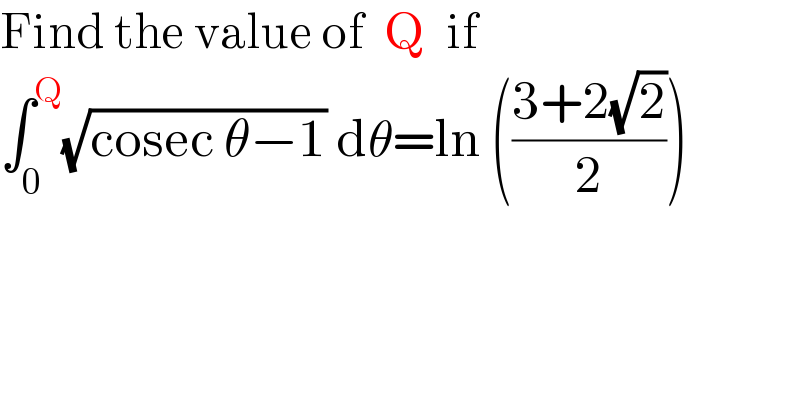
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\:\mathrm{Q}\:\:\mathrm{if} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{Q}} \sqrt{\mathrm{cosec}\:\theta−\mathrm{1}}\:\mathrm{d}\theta=\mathrm{ln}\:\left(\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}}\right) \\ $$$$ \\ $$
Commented by MJS_new last updated on 29/Mar/22

$${dx}? \\ $$
Commented by peter frank last updated on 29/Mar/22

$$\mathrm{d}\theta \\ $$
Answered by MJS_new last updated on 29/Mar/22
![∫(√(csc θ −1))dθ= [t=(√(csc θ −1)) → dθ=−((2dt)/((t^2 +1)(√(t^2 +2))))] =−2∫(t/((t^2 +1)(√(t^2 +2))))= [u=((t+(√(t^2 +2)))/( (√2))) → dt=((√(t^2 +2))/u)] =−2(√2)∫((u^2 −1)/(u^4 +1))du= =∫((2u+(√2))/(u^2 +(√2)u+1))−((2u−(√2))/(u^2 −(√2)u+1)))du= =ln ((u^2 +(√2)u+1)/(u^2 −(√2)u+1)) = ... =ln (1+2sin x +2(√((1+sin x)sin x))) +C this equals 0 with x=0 ⇒ 1+2sin Q +2(√((1+sin Q)sin Q))=((3+2(√2))/2) ⇒ sin Q =((11−6(√2))/8) ...](Q167933.png)
$$\int\sqrt{\mathrm{csc}\:\theta\:−\mathrm{1}}{d}\theta= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\mathrm{csc}\:\theta\:−\mathrm{1}}\:\rightarrow\:{d}\theta=−\frac{\mathrm{2}{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{{t}^{\mathrm{2}} +\mathrm{2}}}\right] \\ $$$$=−\mathrm{2}\int\frac{{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{{t}^{\mathrm{2}} +\mathrm{2}}}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{{t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{2}}}{\:\sqrt{\mathrm{2}}}\:\rightarrow\:{dt}=\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{2}}}{{u}}\right] \\ $$$$=−\mathrm{2}\sqrt{\mathrm{2}}\int\frac{{u}^{\mathrm{2}} −\mathrm{1}}{{u}^{\mathrm{4}} +\mathrm{1}}{du}= \\ $$$$\left.=\int\frac{\mathrm{2}{u}+\sqrt{\mathrm{2}}}{{u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{u}+\mathrm{1}}−\frac{\mathrm{2}{u}−\sqrt{\mathrm{2}}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}+\mathrm{1}}\right){du}= \\ $$$$=\mathrm{ln}\:\frac{{u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{u}+\mathrm{1}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}+\mathrm{1}}\:= \\ $$$$... \\ $$$$=\mathrm{ln}\:\left(\mathrm{1}+\mathrm{2sin}\:{x}\:+\mathrm{2}\sqrt{\left(\mathrm{1}+\mathrm{sin}\:{x}\right)\mathrm{sin}\:{x}}\right)\:+{C} \\ $$$$\mathrm{this}\:\mathrm{equals}\:\mathrm{0}\:\mathrm{with}\:{x}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\mathrm{1}+\mathrm{2sin}\:{Q}\:+\mathrm{2}\sqrt{\left(\mathrm{1}+\mathrm{sin}\:{Q}\right)\mathrm{sin}\:{Q}}=\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{sin}\:{Q}\:=\frac{\mathrm{11}−\mathrm{6}\sqrt{\mathrm{2}}}{\mathrm{8}} \\ $$$$... \\ $$
Answered by peter frank last updated on 29/Mar/22
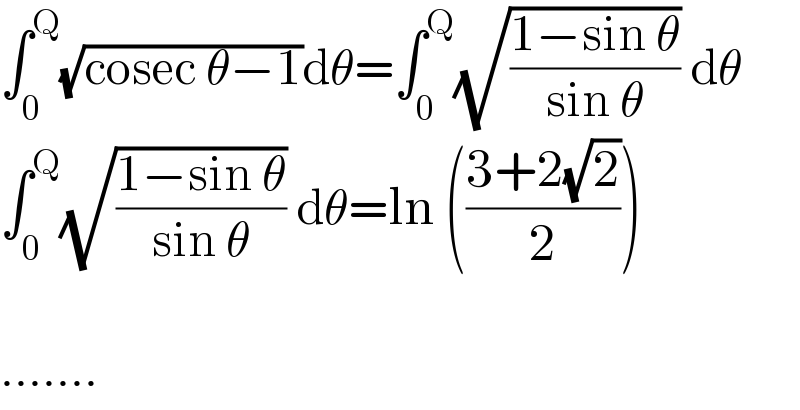
$$\int_{\mathrm{0}} ^{\mathrm{Q}} \sqrt{\mathrm{cosec}\:\theta−\mathrm{1}}\mathrm{d}\theta=\int_{\mathrm{0}} ^{\mathrm{Q}} \sqrt{\frac{\mathrm{1}−\mathrm{sin}\:\theta}{\mathrm{sin}\:\theta}}\:\mathrm{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\mathrm{Q}} \sqrt{\frac{\mathrm{1}−\mathrm{sin}\:\theta}{\mathrm{sin}\:\theta}}\:\mathrm{d}\theta=\mathrm{ln}\:\left(\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}}\right) \\ $$$$ \\ $$$$....... \\ $$
Answered by peter frank last updated on 30/Mar/22
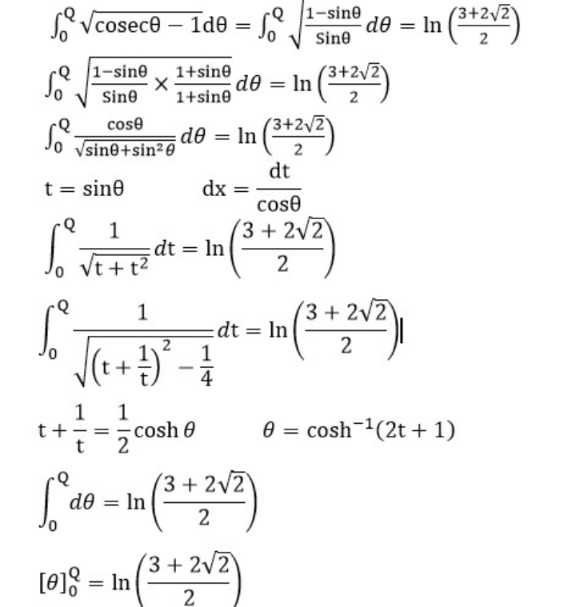
Answered by peter frank last updated on 30/Mar/22
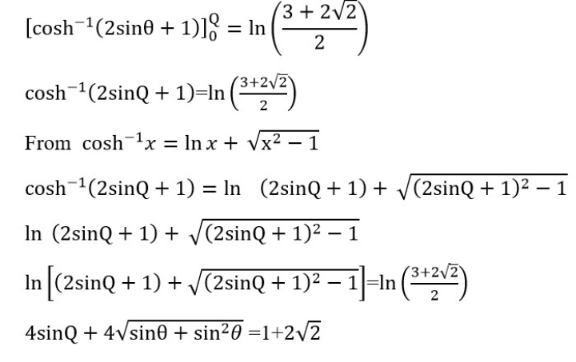
Commented by peter frank last updated on 30/Mar/22

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Mjs}\:\mathrm{for}\:\mathrm{you}\:\mathrm{idea} \\ $$
