
Question Number 167916 by bounhome last updated on 29/Mar/22
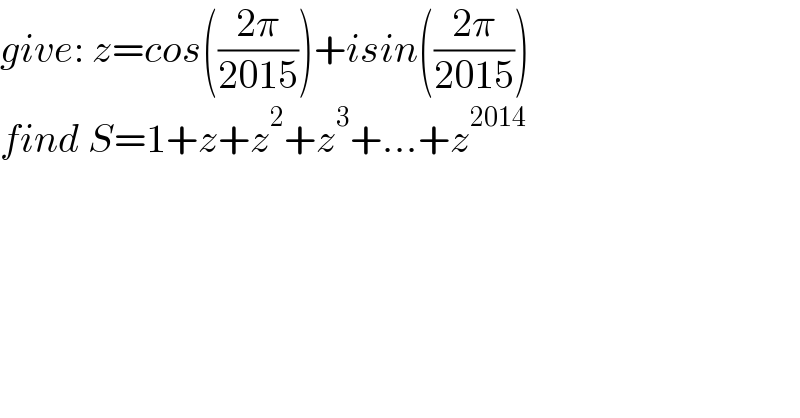
$${give}:\:{z}={cos}\left(\frac{\mathrm{2}\pi}{\mathrm{2015}}\right)+{isin}\left(\frac{\mathrm{2}\pi}{\mathrm{2015}}\right) \\ $$$${find}\:{S}=\mathrm{1}+{z}+{z}^{\mathrm{2}} +{z}^{\mathrm{3}} +...+{z}^{\mathrm{2014}} \\ $$
Commented by benhamimed last updated on 29/Mar/22
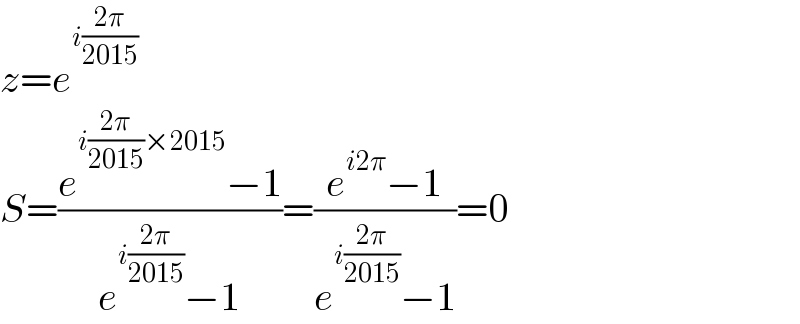
$${z}={e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{2015}}} \\ $$$${S}=\frac{{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{2015}}×\mathrm{2015}} −\mathrm{1}}{{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{2015}}} −\mathrm{1}}=\frac{{e}^{{i}\mathrm{2}\pi} −\mathrm{1}}{{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{2015}}} −\mathrm{1}}=\mathrm{0} \\ $$
Answered by dangduomg last updated on 29/Mar/22
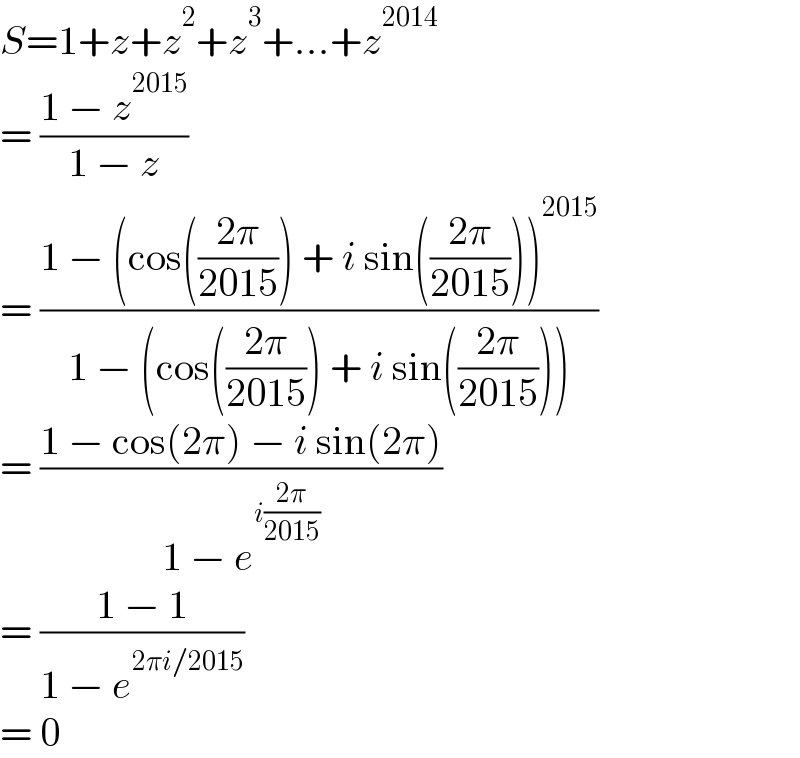
$${S}=\mathrm{1}+{z}+{z}^{\mathrm{2}} +{z}^{\mathrm{3}} +...+{z}^{\mathrm{2014}} \\ $$$$=\:\frac{\mathrm{1}\:−\:{z}^{\mathrm{2015}} }{\mathrm{1}\:−\:{z}} \\ $$$$=\:\frac{\mathrm{1}\:−\:\left(\mathrm{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{2015}}\right)\:+\:{i}\:\mathrm{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{2015}}\right)\right)^{\mathrm{2015}} }{\mathrm{1}\:−\:\left(\mathrm{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{2015}}\right)\:+\:{i}\:\mathrm{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{2015}}\right)\right)} \\ $$$$=\:\frac{\mathrm{1}\:−\:\mathrm{cos}\left(\mathrm{2}\pi\right)\:−\:{i}\:\mathrm{sin}\left(\mathrm{2}\pi\right)}{\mathrm{1}\:−\:{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{2015}}} } \\ $$$$=\:\frac{\mathrm{1}\:−\:\mathrm{1}}{\mathrm{1}\:−\:{e}^{\mathrm{2}\pi{i}/\mathrm{2015}} } \\ $$$$=\:\mathrm{0} \\ $$
