
Question Number 167911 by MathsFan last updated on 29/Mar/22
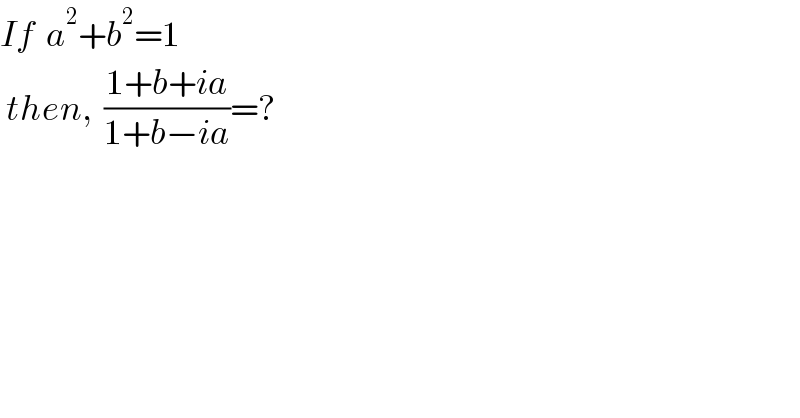
$${If}\:\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{1} \\ $$$$\:{then},\:\:\frac{\mathrm{1}+{b}+{ia}}{\mathrm{1}+{b}−{ia}}=? \\ $$
Answered by MJS_new last updated on 29/Mar/22
![((b+1+ai)/(b+1−ai))=(((b+1+ai)^2 )/((b+1−ai)(b+1+ai)))= =((−a^2 +b^2 +2b+1+2a(b+1)i)/(a^2 +b^2 +2b+1))= [b^2 =1−a^2 ] =((−2a^2 +2b+2+2a(b+1)i)/(2b+2))= =((−a^2 +b+1)/(b+1))+ai= [a^2 =1−b^2 ] =((b^2 +b)/(b+1))+ai= =b+ai](Q167914.png)
$$\frac{{b}+\mathrm{1}+{a}\mathrm{i}}{{b}+\mathrm{1}−{a}\mathrm{i}}=\frac{\left({b}+\mathrm{1}+{a}\mathrm{i}\right)^{\mathrm{2}} }{\left({b}+\mathrm{1}−{a}\mathrm{i}\right)\left({b}+\mathrm{1}+{a}\mathrm{i}\right)}= \\ $$$$=\frac{−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{b}+\mathrm{1}+\mathrm{2}{a}\left({b}+\mathrm{1}\right)\mathrm{i}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{b}+\mathrm{1}}= \\ $$$$\:\:\:\:\:\left[{b}^{\mathrm{2}} =\mathrm{1}−{a}^{\mathrm{2}} \right] \\ $$$$=\frac{−\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{b}+\mathrm{2}+\mathrm{2}{a}\left({b}+\mathrm{1}\right)\mathrm{i}}{\mathrm{2}{b}+\mathrm{2}}= \\ $$$$=\frac{−{a}^{\mathrm{2}} +{b}+\mathrm{1}}{{b}+\mathrm{1}}+{a}\mathrm{i}= \\ $$$$\:\:\:\:\:\left[{a}^{\mathrm{2}} =\mathrm{1}−{b}^{\mathrm{2}} \right] \\ $$$$=\frac{{b}^{\mathrm{2}} +{b}}{{b}+\mathrm{1}}+{a}\mathrm{i}= \\ $$$$={b}+{a}\mathrm{i} \\ $$
Commented by MathsFan last updated on 29/Mar/22

$${thanks} \\ $$
