
Question Number 167838 by cortano1 last updated on 27/Mar/22
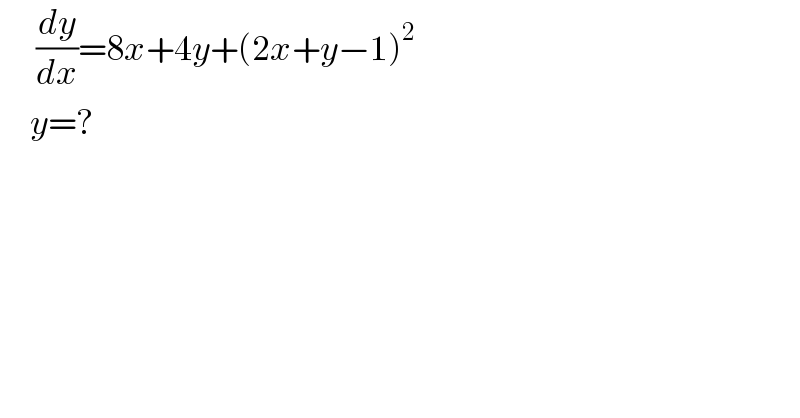
$$\:\:\:\:\:\:\frac{{dy}}{{dx}}=\mathrm{8}{x}+\mathrm{4}{y}+\left(\mathrm{2}{x}+{y}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:{y}=? \\ $$
Answered by mr W last updated on 27/Mar/22
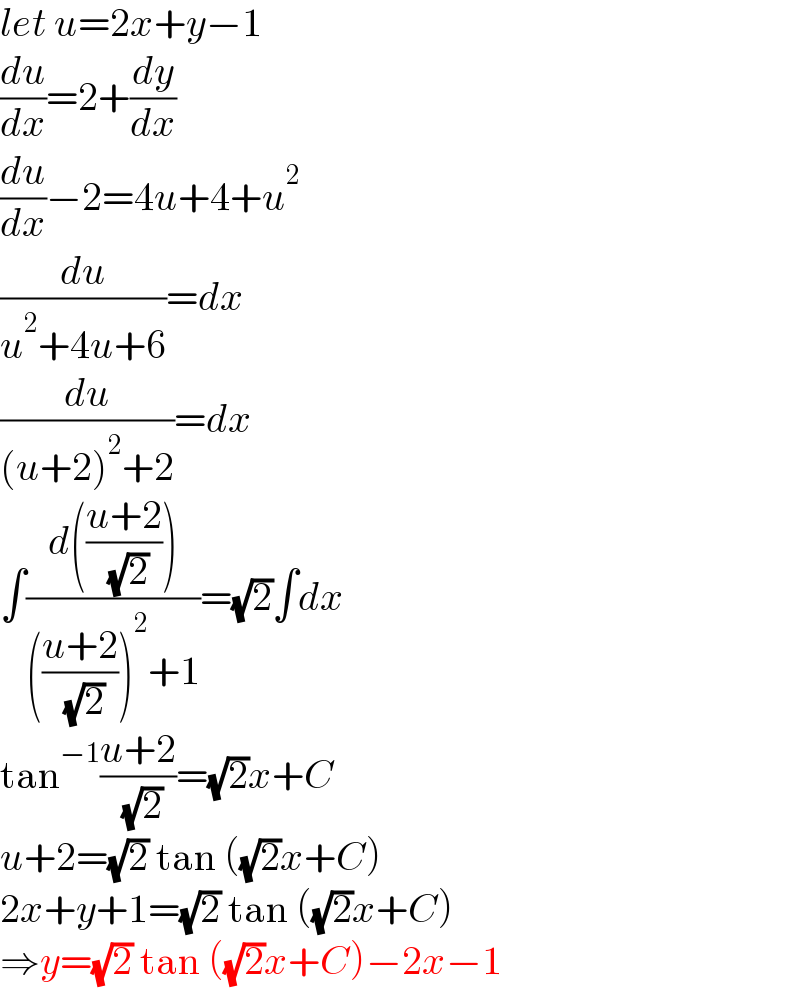
$${let}\:{u}=\mathrm{2}{x}+{y}−\mathrm{1} \\ $$$$\frac{{du}}{{dx}}=\mathrm{2}+\frac{{dy}}{{dx}} \\ $$$$\frac{{du}}{{dx}}−\mathrm{2}=\mathrm{4}{u}+\mathrm{4}+{u}^{\mathrm{2}} \\ $$$$\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{4}{u}+\mathrm{6}}={dx} \\ $$$$\frac{{du}}{\left({u}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{2}}={dx} \\ $$$$\int\frac{{d}\left(\frac{{u}+\mathrm{2}}{\:\sqrt{\mathrm{2}}}\right)}{\left(\frac{{u}+\mathrm{2}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} +\mathrm{1}}=\sqrt{\mathrm{2}}\int{dx} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \frac{{u}+\mathrm{2}}{\:\sqrt{\mathrm{2}}}=\sqrt{\mathrm{2}}{x}+{C} \\ $$$${u}+\mathrm{2}=\sqrt{\mathrm{2}}\:\mathrm{tan}\:\left(\sqrt{\mathrm{2}}{x}+{C}\right) \\ $$$$\mathrm{2}{x}+{y}+\mathrm{1}=\sqrt{\mathrm{2}}\:\mathrm{tan}\:\left(\sqrt{\mathrm{2}}{x}+{C}\right) \\ $$$$\Rightarrow{y}=\sqrt{\mathrm{2}}\:\mathrm{tan}\:\left(\sqrt{\mathrm{2}}{x}+{C}\right)−\mathrm{2}{x}−\mathrm{1} \\ $$
