Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 167821 by mathlove last updated on 26/Mar/22

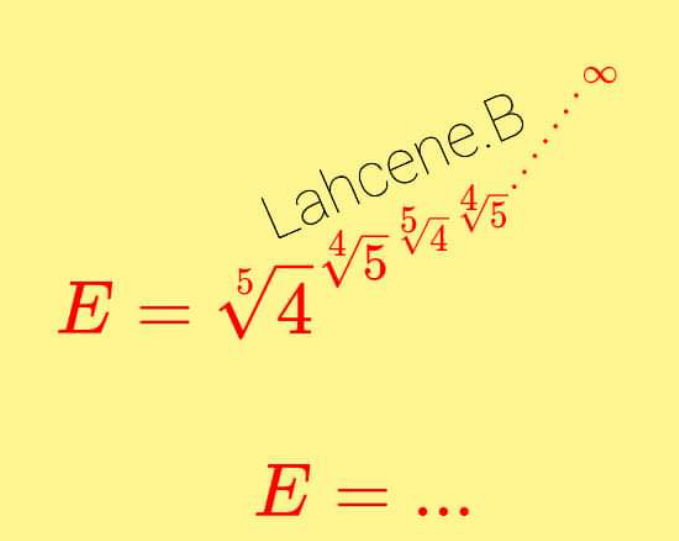
Commented by dangduomg last updated on 26/Mar/22

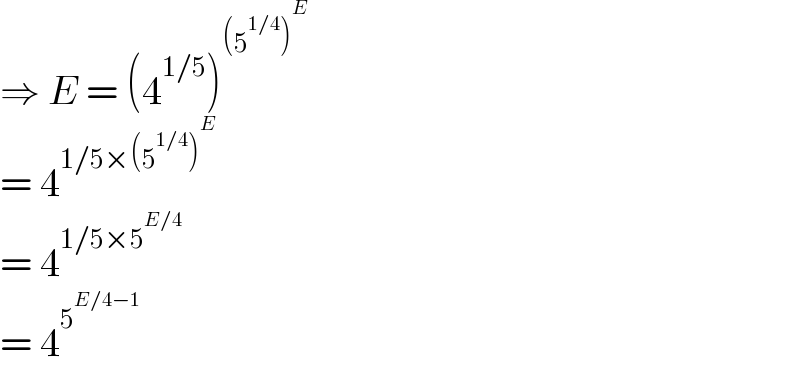
⇒ E = (4^(1/5) )^((5^(1/4) )^E ) = 4^(1/5×(5^(1/4) )^E ) = 4^(1/5×5^(E/4) ) = 4^5^(E/4−1)

$$\Rightarrow\:{E}\:=\:\left(\mathrm{4}^{\mathrm{1}/\mathrm{5}} \right)^{\left(\mathrm{5}^{\mathrm{1}/\mathrm{4}} \right)^{{E}} } \\ $$$$=\:\mathrm{4}^{\mathrm{1}/\mathrm{5}×\left(\mathrm{5}^{\mathrm{1}/\mathrm{4}} \right)^{{E}} } \\ $$$$=\:\mathrm{4}^{\mathrm{1}/\mathrm{5}×\mathrm{5}^{{E}/\mathrm{4}} } \\ $$$$=\:\mathrm{4}^{\mathrm{5}^{{E}/\mathrm{4}−\mathrm{1}} } \\ $$

Commented by aleks041103 last updated on 27/Mar/22

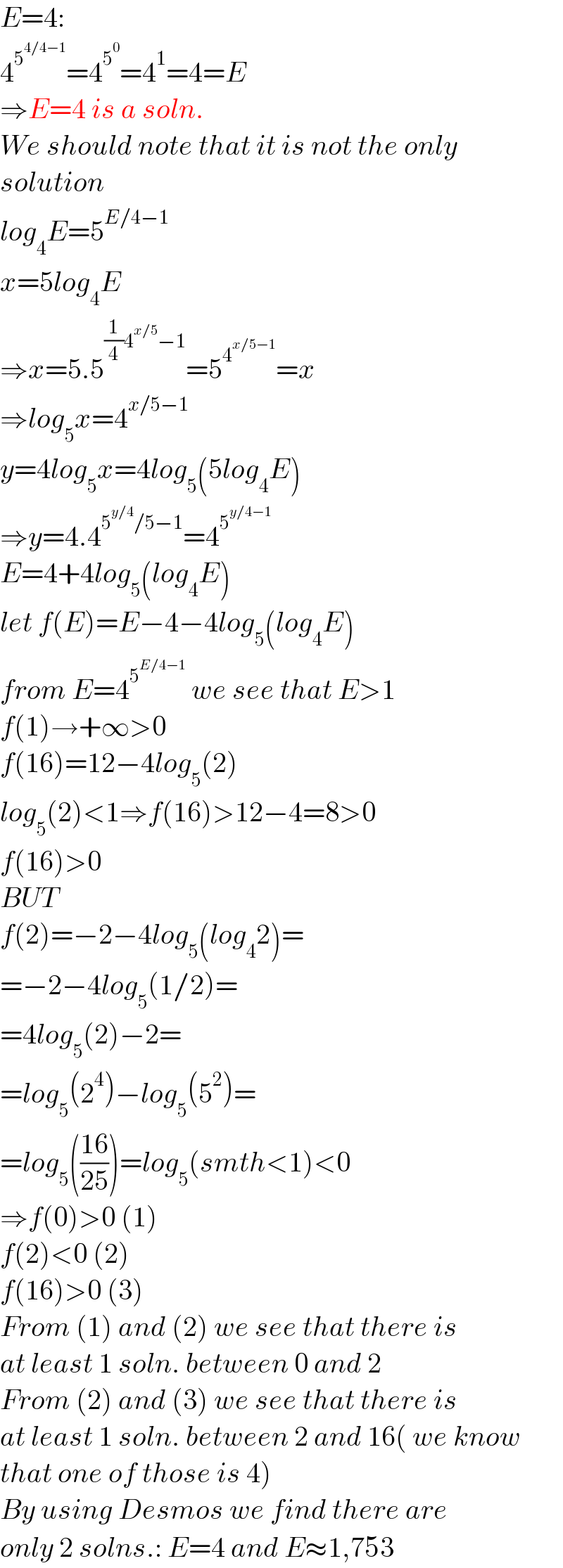
E=4: 4^5^(4/4−1) =4^5^0 =4^1 =4=E ⇒E=4 is a soln. We should note that it is not the only solution log_4 E=5^(E/4−1) x=5log_4 E ⇒x=5.5^((1/4)4^(x/5) −1) =5^4^(x/5−1) =x ⇒log_5 x=4^(x/5−1) y=4log_5 x=4log_5 (5log_4 E) ⇒y=4.4^(5^(y/4) /5−1) =4^5^(y/4−1) E=4+4log_5 (log_4 E) let f(E)=E−4−4log_5 (log_4 E) from E=4^5^(E/4−1) we see that E>1 f(1)→+∞>0 f(16)=12−4log_5 (2) log_5 (2)<1⇒f(16)>12−4=8>0 f(16)>0 BUT f(2)=−2−4log_5 (log_4 2)= =−2−4log_5 (1/2)= =4log_5 (2)−2= =log_5 (2^4 )−log_5 (5^2 )= =log_5 (((16)/(25)))=log_5 (smth<1)<0 ⇒f(0)>0 (1) f(2)<0 (2) f(16)>0 (3) From (1) and (2) we see that there is at least 1 soln. between 0 and 2 From (2) and (3) we see that there is at least 1 soln. between 2 and 16( we know that one of those is 4) By using Desmos we find there are only 2 solns.: E=4 and E≈1,753

$${E}=\mathrm{4}: \\ $$$$\mathrm{4}^{\mathrm{5}^{\mathrm{4}/\mathrm{4}−\mathrm{1}} } =\mathrm{4}^{\mathrm{5}^{\mathrm{0}} } =\mathrm{4}^{\mathrm{1}} =\mathrm{4}={E} \\ $$$$\Rightarrow{E}=\mathrm{4}\:{is}\:{a}\:{soln}. \\ $$$${We}\:{should}\:{note}\:{that}\:{it}\:{is}\:{not}\:{the}\:{only} \\ $$$${solution} \\ $$$${log}_{\mathrm{4}} {E}=\mathrm{5}^{{E}/\mathrm{4}−\mathrm{1}} \\ $$$${x}=\mathrm{5}{log}_{\mathrm{4}} {E} \\ $$$$\Rightarrow{x}=\mathrm{5}.\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{4}}\mathrm{4}^{{x}/\mathrm{5}} −\mathrm{1}} =\mathrm{5}^{\mathrm{4}^{{x}/\mathrm{5}−\mathrm{1}} } ={x} \\ $$$$\Rightarrow{log}_{\mathrm{5}} {x}=\mathrm{4}^{{x}/\mathrm{5}−\mathrm{1}} \\ $$$${y}=\mathrm{4}{log}_{\mathrm{5}} {x}=\mathrm{4}{log}_{\mathrm{5}} \left(\mathrm{5}{log}_{\mathrm{4}} {E}\right) \\ $$$$\Rightarrow{y}=\mathrm{4}.\mathrm{4}^{\mathrm{5}^{{y}/\mathrm{4}} /\mathrm{5}−\mathrm{1}} =\mathrm{4}^{\mathrm{5}^{{y}/\mathrm{4}−\mathrm{1}} } \\ $$$${E}=\mathrm{4}+\mathrm{4}{log}_{\mathrm{5}} \left({log}_{\mathrm{4}} {E}\right) \\ $$$${let}\:{f}\left({E}\right)={E}−\mathrm{4}−\mathrm{4}{log}_{\mathrm{5}} \left({log}_{\mathrm{4}} {E}\right) \\ $$$${from}\:{E}=\mathrm{4}^{\mathrm{5}^{{E}/\mathrm{4}−\mathrm{1}} } \:{we}\:{see}\:{that}\:{E}>\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)\rightarrow+\infty>\mathrm{0} \\ $$$${f}\left(\mathrm{16}\right)=\mathrm{12}−\mathrm{4}{log}_{\mathrm{5}} \left(\mathrm{2}\right) \\ $$$${log}_{\mathrm{5}} \left(\mathrm{2}\right)<\mathrm{1}\Rightarrow{f}\left(\mathrm{16}\right)>\mathrm{12}−\mathrm{4}=\mathrm{8}>\mathrm{0} \\ $$$${f}\left(\mathrm{16}\right)>\mathrm{0} \\ $$$${BUT} \\ $$$${f}\left(\mathrm{2}\right)=−\mathrm{2}−\mathrm{4}{log}_{\mathrm{5}} \left({log}_{\mathrm{4}} \mathrm{2}\right)= \\ $$$$=−\mathrm{2}−\mathrm{4}{log}_{\mathrm{5}} \left(\mathrm{1}/\mathrm{2}\right)= \\ $$$$=\mathrm{4}{log}_{\mathrm{5}} \left(\mathrm{2}\right)−\mathrm{2}= \\ $$$$={log}_{\mathrm{5}} \left(\mathrm{2}^{\mathrm{4}} \right)−{log}_{\mathrm{5}} \left(\mathrm{5}^{\mathrm{2}} \right)= \\ $$$$={log}_{\mathrm{5}} \left(\frac{\mathrm{16}}{\mathrm{25}}\right)={log}_{\mathrm{5}} \left({smth}<\mathrm{1}\right)<\mathrm{0} \\ $$$$\Rightarrow{f}\left(\mathrm{0}\right)>\mathrm{0}\:\left(\mathrm{1}\right) \\ $$$${f}\left(\mathrm{2}\right)<\mathrm{0}\:\left(\mathrm{2}\right) \\ $$$${f}\left(\mathrm{16}\right)>\mathrm{0}\:\left(\mathrm{3}\right) \\ $$$${From}\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right)\:{we}\:{see}\:{that}\:{there}\:{is} \\ $$$${at}\:{least}\:\mathrm{1}\:{soln}.\:{between}\:\mathrm{0}\:{and}\:\mathrm{2} \\ $$$${From}\:\left(\mathrm{2}\right)\:{and}\:\left(\mathrm{3}\right)\:{we}\:{see}\:{that}\:{there}\:{is} \\ $$$${at}\:{least}\:\mathrm{1}\:{soln}.\:{between}\:\mathrm{2}\:{and}\:\mathrm{16}\left(\:{we}\:{know}\right. \\ $$$$\left.{that}\:{one}\:{of}\:{those}\:{is}\:\mathrm{4}\right) \\ $$$${By}\:{using}\:{Desmos}\:{we}\:{find}\:{there}\:{are} \\ $$$${only}\:\mathrm{2}\:{solns}.:\:{E}=\mathrm{4}\:{and}\:{E}\approx\mathrm{1},\mathrm{753} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com