
Question Number 167800 by cortano1 last updated on 25/Mar/22
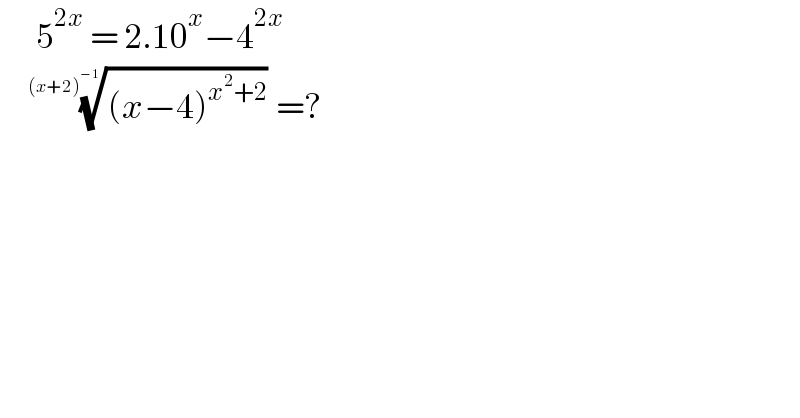
$$\:\:\:\:\:\:\mathrm{5}^{\mathrm{2}{x}} \:=\:\mathrm{2}.\mathrm{10}^{{x}} −\mathrm{4}^{\mathrm{2}{x}} \: \\ $$$$\:\:\:\:\:\sqrt[{\left({x}+\mathrm{2}\right)^{−\mathrm{1}} }]{\left({x}−\mathrm{4}\right)^{{x}^{\mathrm{2}} +\mathrm{2}} }=?\: \\ $$
Commented by MJS_new last updated on 25/Mar/22

$${x}=\mathrm{0} \\ $$
Commented by logan whetzel last updated on 26/Mar/22
please explain this awnser
Commented by MJS_new last updated on 26/Mar/22
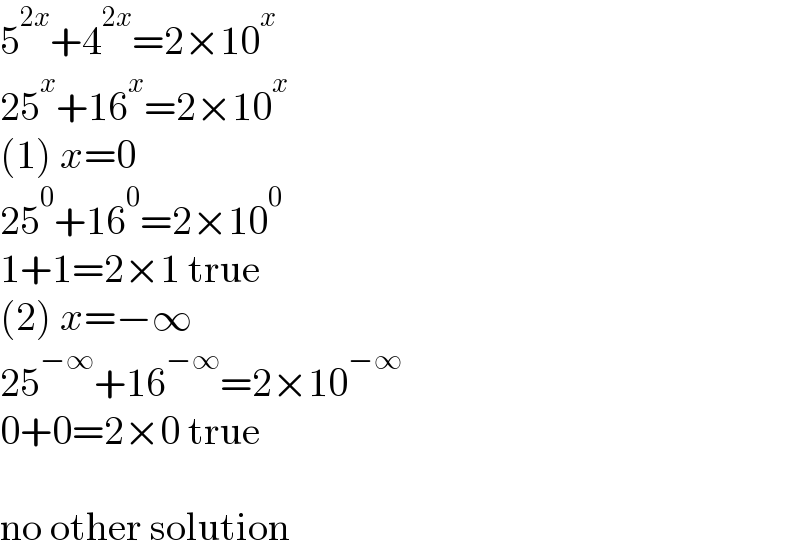
$$\mathrm{5}^{\mathrm{2}{x}} +\mathrm{4}^{\mathrm{2}{x}} =\mathrm{2}×\mathrm{10}^{{x}} \\ $$$$\mathrm{25}^{{x}} +\mathrm{16}^{{x}} =\mathrm{2}×\mathrm{10}^{{x}} \\ $$$$\left(\mathrm{1}\right)\:{x}=\mathrm{0} \\ $$$$\mathrm{25}^{\mathrm{0}} +\mathrm{16}^{\mathrm{0}} =\mathrm{2}×\mathrm{10}^{\mathrm{0}} \\ $$$$\mathrm{1}+\mathrm{1}=\mathrm{2}×\mathrm{1}\:\mathrm{true} \\ $$$$\left(\mathrm{2}\right)\:{x}=−\infty \\ $$$$\mathrm{25}^{−\infty} +\mathrm{16}^{−\infty} =\mathrm{2}×\mathrm{10}^{−\infty} \\ $$$$\mathrm{0}+\mathrm{0}=\mathrm{2}×\mathrm{0}\:\mathrm{true} \\ $$$$ \\ $$$$\mathrm{no}\:\mathrm{other}\:\mathrm{solution} \\ $$
