
Question Number 167776 by peter frank last updated on 24/Mar/22
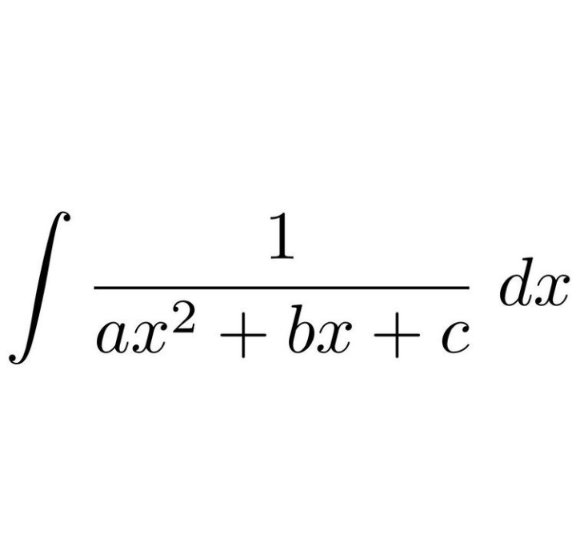
Answered by MikeH last updated on 24/Mar/22
![ax^2 +bx +c = a(x^2 +(b/a)x + (c/a)) = a[(x+(b/(2a)))^2 −(b^2 /(4a^2 ))+(c/a)] = a[(x+(b/(2a)))^2 +((−b^2 +4ac)/(4a^2 ))] = a(x+(b/(2a)))^2 +((4ac−b^2 )/(4a)) ∫(1/(a(x+(b/(2a)))^2 +((4ac−b^2 )/(4a)))) dx Let u = x + (b/(2a)) ⇒ du = dx ∫(1/(au^2 +k))du , where k = ((4ac−b^2 )/(4a)) ∫(1/(a(u^2 +((√(k/a)))^2 )))du = (1/a)(√(a/k)) tan^(−1) (x(√(a/k))) +p.](Q167779.png)
$${ax}^{\mathrm{2}} +{bx}\:+{c}\:=\:{a}\left({x}^{\mathrm{2}} +\frac{{b}}{{a}}{x}\:+\:\frac{{c}}{{a}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{a}\left[\left({x}+\frac{{b}}{\mathrm{2}{a}}\right)^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }+\frac{{c}}{{a}}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{a}\left[\left({x}+\frac{{b}}{\mathrm{2}{a}}\right)^{\mathrm{2}} +\frac{−{b}^{\mathrm{2}} +\mathrm{4}{ac}}{\mathrm{4}{a}^{\mathrm{2}} }\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{a}\left({x}+\frac{{b}}{\mathrm{2}{a}}\right)^{\mathrm{2}} +\frac{\mathrm{4}{ac}−{b}^{\mathrm{2}} }{\mathrm{4}{a}} \\ $$$$\int\frac{\mathrm{1}}{{a}\left({x}+\frac{{b}}{\mathrm{2}{a}}\right)^{\mathrm{2}} +\frac{\mathrm{4}{ac}−{b}^{\mathrm{2}} }{\mathrm{4}{a}}}\:{dx} \\ $$$$\mathrm{Let}\:{u}\:=\:{x}\:+\:\frac{{b}}{\mathrm{2}{a}}\:\Rightarrow\:{du}\:=\:{dx} \\ $$$$\int\frac{\mathrm{1}}{{au}^{\mathrm{2}} +{k}}{du}\:,\:\:\mathrm{where}\:{k}\:=\:\frac{\mathrm{4}{ac}−{b}^{\mathrm{2}} }{\mathrm{4}{a}} \\ $$$$\int\frac{\mathrm{1}}{{a}\left({u}^{\mathrm{2}} +\left(\sqrt{\frac{{k}}{{a}}}\right)^{\mathrm{2}} \right)}{du}\:=\:\frac{\mathrm{1}}{{a}}\sqrt{\frac{{a}}{{k}}}\:\mathrm{tan}^{−\mathrm{1}} \left({x}\sqrt{\frac{{a}}{{k}}}\right)\:+{p}. \\ $$$$ \\ $$
Commented by peter frank last updated on 26/Mar/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by MJS_new last updated on 25/Mar/22
![∫(dx/(ax^2 +bx+c))= [t=2ax+b → dx=(dt/(2a))] =2∫(dt/(t^2 +4ac−b^2 )) (1) 4ac−b^2 <0 ⇒ 4ac−b^2 =−d^2 ∧d>0 2∫(dt/(t^2 +4ac−b^2 ))=2∫(dt/(t^2 −d^2 ))=2∫(dt/((t−d)(t+d)))= =(1/d)∫((1/(t−d))−(1/(t+d)))dt=((ln (t−d) −ln (t+d))/d)= =((ln ∣2ax+b−(√(b^2 −4ac))∣ −ln ∣2ax+b+(√(b^2 −4ax))∣)/( (√(b^2 −4ac))))+C (2) 4ac−b^2 =0 2∫(dt/t^2 )=−(2/t)=−(2/(2ax+b))+C (3) 4ac−b^2 >0 ⇒ 4ac−b^2 =d^2 ∧d>0 2∫(dt/(t^2 +4ac−b^2 ))=2∫(dt/(t^2 +d^2 ))= =((2arctan (t/d))/d)= =((2arctan ((2ax+b)/( (√(4ac−b^2 )))))/( (√(4ac−b^2 ))))+C](Q167799.png)
$$\int\frac{{dx}}{{ax}^{\mathrm{2}} +{bx}+{c}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{2}{ax}+{b}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{2}{a}}\right] \\ $$$$=\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{4}{ac}−{b}^{\mathrm{2}} } \\ $$$$\left(\mathrm{1}\right)\:\mathrm{4}{ac}−{b}^{\mathrm{2}} <\mathrm{0}\:\Rightarrow\:\mathrm{4}{ac}−{b}^{\mathrm{2}} =−{d}^{\mathrm{2}} \wedge{d}>\mathrm{0} \\ $$$$\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{4}{ac}−{b}^{\mathrm{2}} }=\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} −{d}^{\mathrm{2}} }=\mathrm{2}\int\frac{{dt}}{\left({t}−{d}\right)\left({t}+{d}\right)}= \\ $$$$=\frac{\mathrm{1}}{{d}}\int\left(\frac{\mathrm{1}}{{t}−{d}}−\frac{\mathrm{1}}{{t}+{d}}\right){dt}=\frac{\mathrm{ln}\:\left({t}−{d}\right)\:−\mathrm{ln}\:\left({t}+{d}\right)}{{d}}= \\ $$$$=\frac{\mathrm{ln}\:\mid\mathrm{2}{ax}+{b}−\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}\mid\:−\mathrm{ln}\:\mid\mathrm{2}{ax}+{b}+\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ax}}\mid}{\:\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}+{C} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{4}{ac}−{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} }=−\frac{\mathrm{2}}{{t}}=−\frac{\mathrm{2}}{\mathrm{2}{ax}+{b}}+{C} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{4}{ac}−{b}^{\mathrm{2}} >\mathrm{0}\:\Rightarrow\:\mathrm{4}{ac}−{b}^{\mathrm{2}} ={d}^{\mathrm{2}} \wedge{d}>\mathrm{0} \\ $$$$\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{4}{ac}−{b}^{\mathrm{2}} }=\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} +{d}^{\mathrm{2}} }= \\ $$$$=\frac{\mathrm{2arctan}\:\frac{{t}}{{d}}}{{d}}= \\ $$$$=\frac{\mathrm{2arctan}\:\frac{\mathrm{2}{ax}+{b}}{\:\sqrt{\mathrm{4}{ac}−{b}^{\mathrm{2}} }}}{\:\sqrt{\mathrm{4}{ac}−{b}^{\mathrm{2}} }}+{C} \\ $$
Commented by peter frank last updated on 26/Mar/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by MJS_new last updated on 27/Mar/22

$$\mathrm{hey}\:\mathrm{Peter},\:\mathrm{you}'\mathrm{re}\:\mathrm{welcome}!\:\mathrm{regards}\:\mathrm{from} \\ $$$$\mathrm{Vienna}\:\left(\mathrm{Austria}\right),\:\mathrm{Martin} \\ $$
