
Question Number 167739 by DAVONG last updated on 24/Mar/22
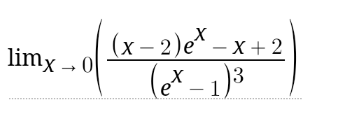
Commented by mkam last updated on 24/Mar/22

$$−\infty \\ $$
Commented by mkam last updated on 24/Mar/22

$$−\infty \\ $$
Answered by Nimatullah last updated on 24/Mar/22

$$\mathrm{1} \\ $$
Answered by LEKOUMA last updated on 24/Mar/22
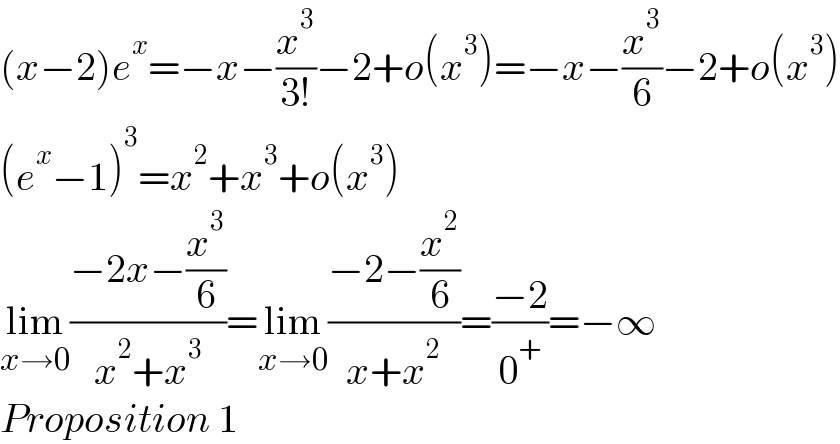
$$\left({x}−\mathrm{2}\right){e}^{{x}} =−{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}−\mathrm{2}+{o}\left({x}^{\mathrm{3}} \right)=−{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}−\mathrm{2}+{o}\left({x}^{\mathrm{3}} \right) \\ $$$$\left({e}^{{x}} −\mathrm{1}\right)^{\mathrm{3}} ={x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{o}\left({x}^{\mathrm{3}} \right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2}{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}{{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}}{{x}+{x}^{\mathrm{2}} }=\frac{−\mathrm{2}}{\mathrm{0}^{+} }=−\infty \\ $$$${Proposition}\:\mathrm{1} \\ $$
Answered by LEKOUMA last updated on 24/Mar/22
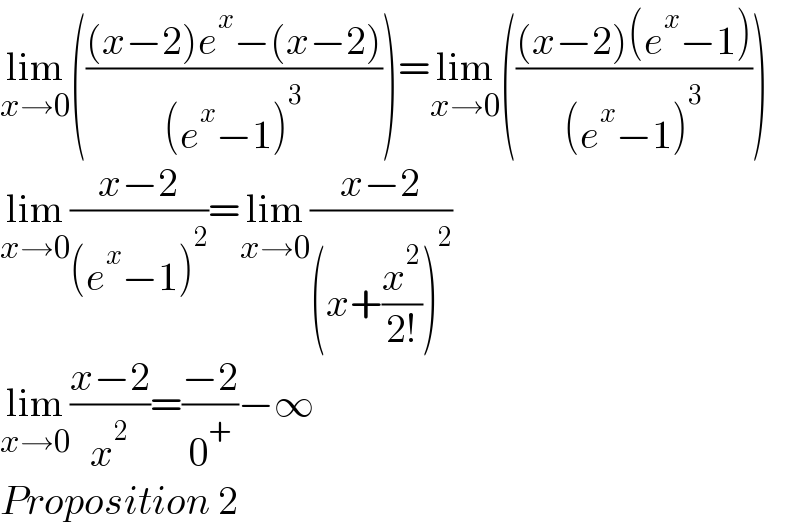
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left({x}−\mathrm{2}\right){e}^{{x}} −\left({x}−\mathrm{2}\right)}{\left({e}^{{x}} −\mathrm{1}\right)^{\mathrm{3}} }\right)=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left({x}−\mathrm{2}\right)\left({e}^{{x}} −\mathrm{1}\right)}{\left({e}^{{x}} −\mathrm{1}\right)^{\mathrm{3}} }\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−\mathrm{2}}{\left({e}^{{x}} −\mathrm{1}\right)^{\mathrm{2}} }=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−\mathrm{2}}{\left({x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}\right)^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} }=\frac{−\mathrm{2}}{\mathrm{0}^{+} }−\infty \\ $$$${Proposition}\:\mathrm{2} \\ $$
Answered by greogoury55 last updated on 24/Mar/22
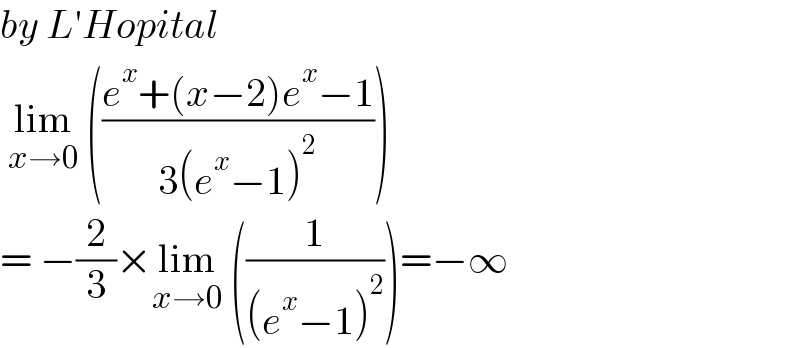
$${by}\:{L}'{Hopital} \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{{e}^{{x}} +\left({x}−\mathrm{2}\right){e}^{{x}} −\mathrm{1}}{\mathrm{3}\left({e}^{{x}} −\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$=\:−\frac{\mathrm{2}}{\mathrm{3}}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\left({e}^{{x}} −\mathrm{1}\right)^{\mathrm{2}} }\right)=−\infty \\ $$
