
Question Number 167716 by cortano1 last updated on 23/Mar/22

Answered by mahdipoor last updated on 23/Mar/22
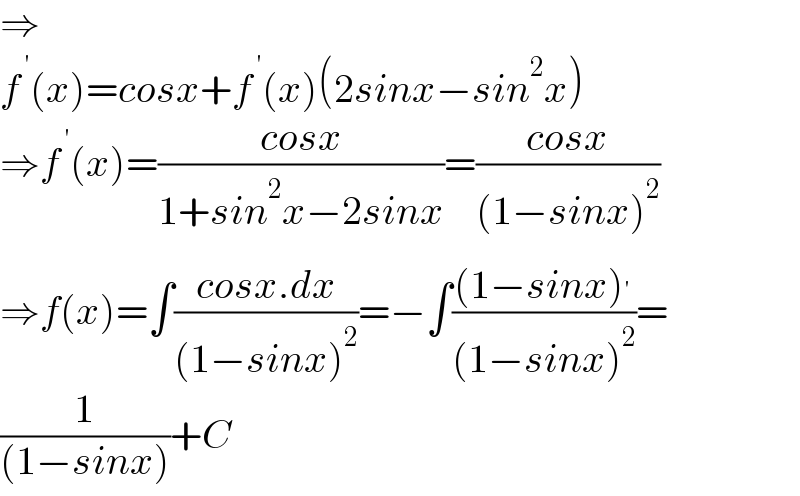
$$\Rightarrow \\ $$$${f}^{\:'} \left({x}\right)={cosx}+{f}^{\:'} \left({x}\right)\left(\mathrm{2}{sinx}−{sin}^{\mathrm{2}} {x}\right) \\ $$$$\Rightarrow{f}^{\:'} \left({x}\right)=\frac{{cosx}}{\mathrm{1}+{sin}^{\mathrm{2}} {x}−\mathrm{2}{sinx}}=\frac{{cosx}}{\left(\mathrm{1}−{sinx}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{f}\left({x}\right)=\int\frac{{cosx}.{dx}}{\left(\mathrm{1}−{sinx}\right)^{\mathrm{2}} }=−\int\frac{\left(\mathrm{1}−{sinx}\right)^{'} }{\left(\mathrm{1}−{sinx}\right)^{\mathrm{2}} }= \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}−{sinx}\right)}+{C} \\ $$
