
Question Number 167666 by LEKOUMA last updated on 22/Mar/22
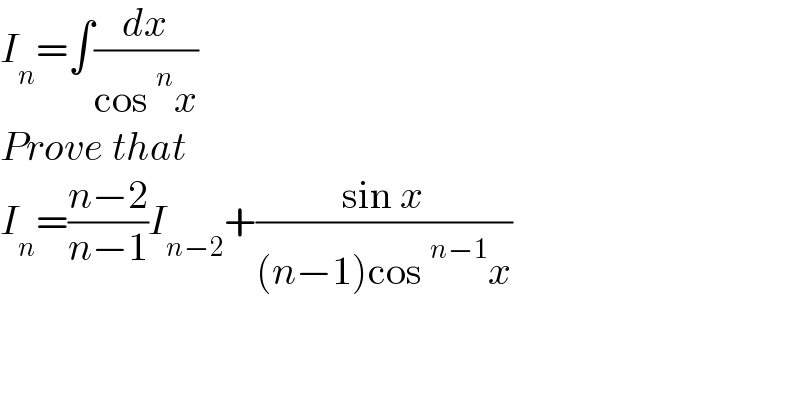
$${I}_{{n}} =\int\frac{{dx}}{\mathrm{cos}\:^{{n}} {x}} \\ $$$${Prove}\:{that} \\ $$$${I}_{{n}} =\frac{{n}−\mathrm{2}}{{n}−\mathrm{1}}{I}_{{n}−\mathrm{2}} +\frac{\mathrm{sin}\:{x}}{\left({n}−\mathrm{1}\right)\mathrm{cos}\:^{{n}−\mathrm{1}} {x}} \\ $$
Commented by peter frank last updated on 22/Mar/22

$$\mathrm{Reduction}\:\mathrm{formular}\: \\ $$
Answered by chhaythean last updated on 22/Mar/22

$$\mathrm{Solution} \\ $$$$\mathrm{I}_{\mathrm{n}} =\int\frac{\mathrm{dx}}{\mathrm{cos}^{\mathrm{n}} \mathrm{x}}=\int\mathrm{sec}^{\mathrm{n}} \mathrm{xdx} \\ $$$$=\int\mathrm{sec}^{\mathrm{n}−\mathrm{2}} \mathrm{xsec}^{\mathrm{2}} \mathrm{xdx} \\ $$$$\mathrm{let}\:\begin{cases}{\mathrm{u}=\mathrm{sec}^{\mathrm{n}−\mathrm{2}} \mathrm{x}\Rightarrow\mathrm{du}=\left(\mathrm{n}−\mathrm{2}\right)\mathrm{sec}^{\mathrm{n}−\mathrm{2}} \mathrm{xtanxdx}}\\{\mathrm{dv}=\mathrm{sec}^{\mathrm{2}} \mathrm{xdx}\Rightarrow\mathrm{v}=\mathrm{tanx}}\end{cases} \\ $$$$\mathrm{I}_{\mathrm{n}} =\mathrm{sec}^{\mathrm{n}−\mathrm{2}} \mathrm{xtanx}−\left(\mathrm{n}−\mathrm{2}\right)\int\mathrm{sec}^{\mathrm{n}−\mathrm{2}} \mathrm{xtan}^{\mathrm{2}} \mathrm{xdx} \\ $$$$=\mathrm{sec}^{\mathrm{n}−\mathrm{2}} \mathrm{xtanx}−\left(\mathrm{n}−\mathrm{2}\right)\int\mathrm{sec}^{\mathrm{n}} \mathrm{xdx}+\left(\mathrm{n}−\mathrm{2}\right)\int\mathrm{sec}^{\mathrm{n}−\mathrm{2}} \mathrm{dx} \\ $$$$\mathrm{I}_{\mathrm{n}} =\mathrm{sec}^{\mathrm{n}−\mathrm{2}} \mathrm{xtanx}−\left(\mathrm{n}−\mathrm{2}\right)\mathrm{I}_{\mathrm{n}} +\left(\mathrm{n}−\mathrm{2}\right)\mathrm{I}_{\mathrm{n}−\mathrm{2}} \\ $$$$\mathrm{I}_{\mathrm{n}} +\left(\mathrm{n}−\mathrm{2}\right)\mathrm{I}_{\mathrm{n}} =\mathrm{sec}^{\mathrm{n}−\mathrm{2}} \mathrm{xtanx}+\left(\mathrm{n}−\mathrm{2}\right)\mathrm{I}_{\mathrm{n}−\mathrm{2}} \\ $$$$\left(\mathrm{n}−\mathrm{1}\right)\mathrm{I}_{\mathrm{n}} =\mathrm{sec}^{\mathrm{n}−\mathrm{2}} \mathrm{xtanx}+\left(\mathrm{n}−\mathrm{2}\right)\mathrm{I}_{\mathrm{n}−\mathrm{2}} \\ $$$$\mathrm{I}_{\mathrm{n}} =\frac{\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{n}−\mathrm{2}} \mathrm{x}}×\frac{\mathrm{sinx}}{\mathrm{cosx}}}{\mathrm{n}−\mathrm{1}}+\frac{\mathrm{n}−\mathrm{2}}{\mathrm{n}−\mathrm{1}}\mathrm{I}_{\mathrm{n}−\mathrm{2}} \\ $$$$\mathrm{I}_{\mathrm{n}} =\frac{\mathrm{n}−\mathrm{2}}{\mathrm{n}−\mathrm{1}}\mathrm{I}_{\mathrm{n}−\mathrm{2}} +\frac{\mathrm{sinx}}{\mathrm{cos}^{\mathrm{n}−\mathrm{1}} \mathrm{x}\left(\mathrm{n}−\mathrm{1}\right)}\:\mathrm{true} \\ $$$$\mathrm{So}\:\begin{array}{|c|}{\mathrm{I}_{\mathrm{n}} =\frac{\mathrm{n}−\mathrm{2}}{\mathrm{n}−\mathrm{1}}\mathrm{I}_{\mathrm{n}−\mathrm{2}} +\frac{\mathrm{sinx}}{\left(\mathrm{n}−\mathrm{1}\right)\mathrm{cos}^{\mathrm{n}−\mathrm{1}} \mathrm{x}}\:\mathrm{is}\:\mathrm{proved}.}\\\hline\end{array} \\ $$
Commented by LEKOUMA last updated on 22/Mar/22

$${Thanks} \\ $$
