
Question Number 167594 by infinityaction last updated on 20/Mar/22
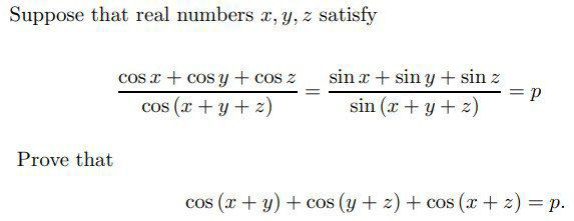
Answered by som(math1967) last updated on 20/Mar/22

$${cosx}+{cosy}+{cosz}={pcos}\left({x}+{y}+{z}\right) \\ $$$${cosxcos}\left({x}+{y}+{z}\right)+{cosycos}\left({x}+{y}+{z}\right) \\ $$$$+{coszcos}\left({x}+{y}+{z}\right)={pcos}^{\mathrm{2}} \left({x}+{y}+{z}\right) \\ $$$$\left.........{case}\:\:{i}\right) \\ $$$${same}\:{way} \\ $$$${sinxsin}\left({x}+{y}+{z}\right)+{sinysin}\left({x}+{y}+{z}\right) \\ $$$$+{sinzsin}\left({x}+{y}+{z}\right)={psin}^{\mathrm{2}} \left({x}+{y}+{z}\right) \\ $$$$\left........{case}\:{ii}\right) \\ $$$$\left.{c}\left.{asei}\right)+{caseii}\right) \\ $$$${cosxcos}\left({x}+{y}+{z}\right)+{sinxsin}\left({x}+{y}+{z}\right) \\ $$$$+{cosycos}\left({x}+{y}+{z}\right)+{sinysin}\left({x}+{y}+{z}\right) \\ $$$${coszcos}\left({x}+{y}+{z}\right)+{sinzsin}\left({x}+{y}+{z}\right) \\ $$$$={p}\left\{{sin}^{\mathrm{2}} \left({x}+{y}+{z}\right)+{cos}^{\mathrm{2}} \left({x}+{y}+{z}\right)\right\} \\ $$$${cos}\left({x}+{y}+{z}−{x}\right)+{cos}\left({x}+{y}+{z}−{y}\right) \\ $$$$+{cos}\left({x}+{y}+{z}−{z}\right)={p}×\mathrm{1} \\ $$$$\therefore\boldsymbol{{cos}}\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)+\boldsymbol{{cos}}\left(\boldsymbol{{y}}+\boldsymbol{{z}}\right)+\boldsymbol{{cos}}\left(\boldsymbol{{z}}+\boldsymbol{{x}}\right)=\boldsymbol{{p}} \\ $$
