
Question Number 167586 by cortano1 last updated on 20/Mar/22
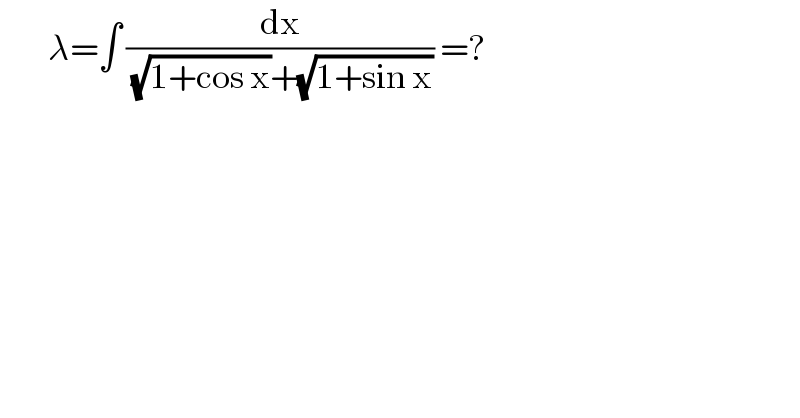
$$\:\:\:\:\:\:\:\:\lambda=\int\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{cos}\:\mathrm{x}}+\sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}}\:=? \\ $$
Commented by MJS_new last updated on 20/Mar/22
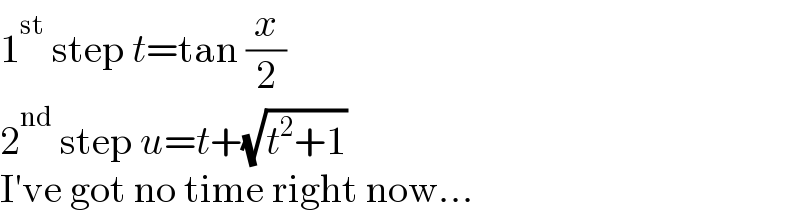
$$\mathrm{1}^{\mathrm{st}} \:\mathrm{step}\:{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}} \\ $$$$\mathrm{2}^{\mathrm{nd}} \:\mathrm{step}\:{u}={t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{I}'\mathrm{ve}\:\mathrm{got}\:\mathrm{no}\:\mathrm{time}\:\mathrm{right}\:\mathrm{now}... \\ $$
Answered by greogoury55 last updated on 20/Mar/22
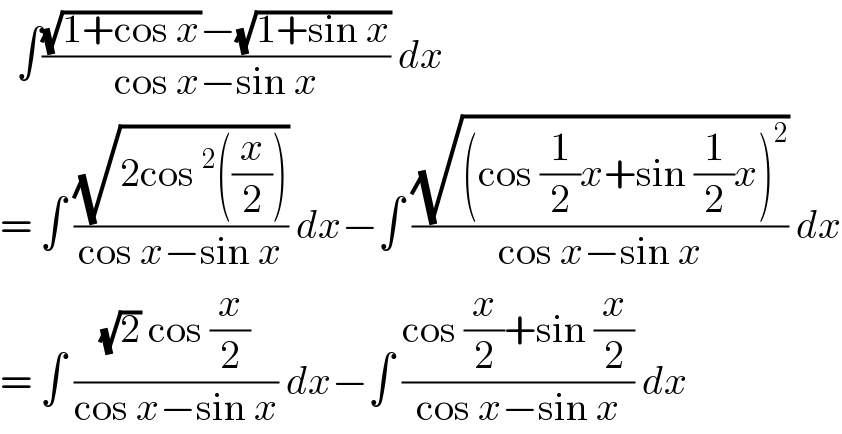
$$\:\:\int\frac{\sqrt{\mathrm{1}+\mathrm{cos}\:{x}}−\sqrt{\mathrm{1}+\mathrm{sin}\:{x}}}{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}\:{dx}\: \\ $$$$=\:\int\:\frac{\sqrt{\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}}{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}\:{dx}−\int\:\frac{\sqrt{\left(\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}{x}+\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}{x}\right)^{\mathrm{2}} }}{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}\:{dx} \\ $$$$=\:\int\:\frac{\sqrt{\mathrm{2}}\:\mathrm{cos}\:\frac{{x}}{\mathrm{2}}}{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}\:{dx}−\int\:\frac{\mathrm{cos}\:\frac{{x}}{\mathrm{2}}+\mathrm{sin}\:\frac{{x}}{\mathrm{2}}}{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}\:{dx}\: \\ $$
Answered by MJS_new last updated on 20/Mar/22
![∫(dx/( (√(1+cos x))+(√(1+sin x))))= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =2∫(dt/((t+1+(√2))(√(t^2 +1))))= [u=t+(√(t^2 +1)) → dt=((√(t^2 +1))/u)du] =4∫(du/(u^2 +2(1+(√2))u−1))= =(√(2−(√2)))ln ((u+1+(√2)−(√(4+2(√2))))/(u+1+(√2)+(√(4+2(√2))))) =...](Q167610.png)
$$\int\frac{{dx}}{\:\sqrt{\mathrm{1}+\mathrm{cos}\:{x}}+\sqrt{\mathrm{1}+\mathrm{sin}\:{x}}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\mathrm{2}\int\frac{{dt}}{\left({t}+\mathrm{1}+\sqrt{\mathrm{2}}\right)\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{u}={t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{dt}=\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{{u}}{du}\right] \\ $$$$=\mathrm{4}\int\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){u}−\mathrm{1}}= \\ $$$$=\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}\mathrm{ln}\:\frac{{u}+\mathrm{1}+\sqrt{\mathrm{2}}−\sqrt{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}}}{{u}+\mathrm{1}+\sqrt{\mathrm{2}}+\sqrt{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}}}\:=... \\ $$
Commented by peter frank last updated on 21/Mar/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
