
Question Number 167576 by mkam last updated on 19/Mar/22
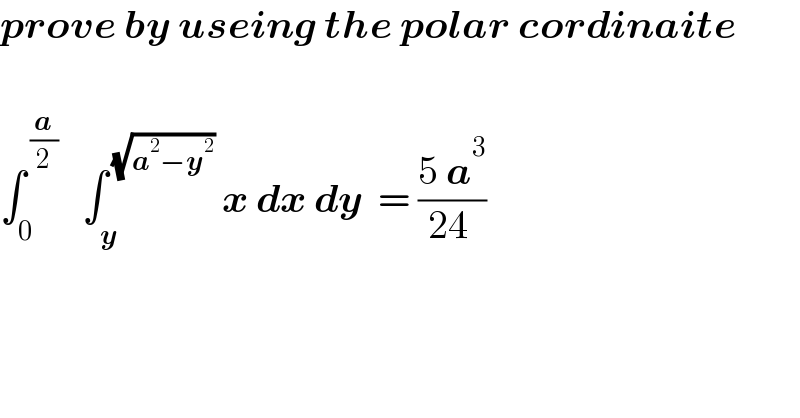
$$\boldsymbol{{prove}}\:\boldsymbol{{by}}\:\boldsymbol{{useing}}\:\boldsymbol{{the}}\:\boldsymbol{{polar}}\:\boldsymbol{{cordinaite}}\: \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\:\frac{\boldsymbol{{a}}}{\mathrm{2}}} \:\:\:\int_{\boldsymbol{{y}}} ^{\:\sqrt{\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{y}}^{\mathrm{2}} }} \:\boldsymbol{{x}}\:\boldsymbol{{dx}}\:\boldsymbol{{dy}}\:\:=\:\frac{\mathrm{5}\:\boldsymbol{{a}}^{\mathrm{3}} }{\mathrm{24}\:} \\ $$
Commented by mkam last updated on 20/Mar/22

$$????? \\ $$
Answered by ArielVyny last updated on 19/Mar/22
![∫_0 ^(a/2) [(1/2)x^2 ]_y ^(√(a^2 −y^2 )) dy=∫_0 ^(a/2) (1/2)a^2 −y^2 =(1/2)a^2 [(a/2)]−(1/3)[(a^3 /8)]=((6a^3 )/(24))−(a^3 /(24))=((5a^3 )/(24))](Q167579.png)
$$\int_{\mathrm{0}} ^{\frac{{a}}{\mathrm{2}}} \left[\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \right]_{{y}} ^{\sqrt{{a}^{\mathrm{2}} −{y}^{\mathrm{2}} }} {dy}=\int_{\mathrm{0}} ^{\frac{{a}}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2}}{a}^{\mathrm{2}} −{y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}{a}^{\mathrm{2}} \left[\frac{{a}}{\mathrm{2}}\right]−\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{{a}^{\mathrm{3}} }{\mathrm{8}}\right]=\frac{\mathrm{6}{a}^{\mathrm{3}} }{\mathrm{24}}−\frac{{a}^{\mathrm{3}} }{\mathrm{24}}=\frac{\mathrm{5}{a}^{\mathrm{3}} }{\mathrm{24}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by ArielVyny last updated on 19/Mar/22
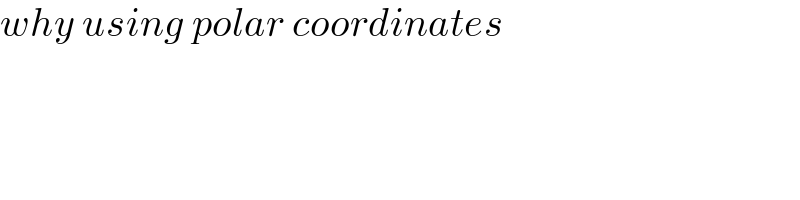
$${why}\:{using}\:{polar}\:{coordinates} \\ $$
Commented by mkam last updated on 19/Mar/22
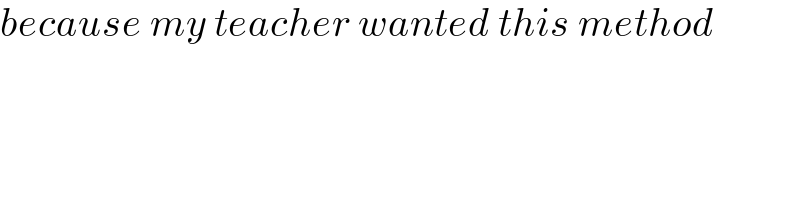
$${because}\:{my}\:{teacher}\:{wanted}\:{this}\:{method} \\ $$
Commented by JDamian last updated on 19/Mar/22
Oh, what kind of you for doing his homework
