
Question Number 16756 by Tinkutara last updated on 26/Jun/17

$$\mathrm{Alternate}\:\mathrm{vertices}\:\mathrm{of}\:\mathrm{a}\:\mathrm{regular}\:\mathrm{hexagon} \\ $$$$\mathrm{are}\:\mathrm{joined}\:\mathrm{as}\:\mathrm{shown}.\:\mathrm{What}\:\mathrm{fraction}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{total}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{hexagon}\:\mathrm{is} \\ $$$$\mathrm{shaded}?\:\left(\mathrm{Justify}\:\mathrm{your}\:\mathrm{answer}.\right) \\ $$
Commented by Tinkutara last updated on 26/Jun/17
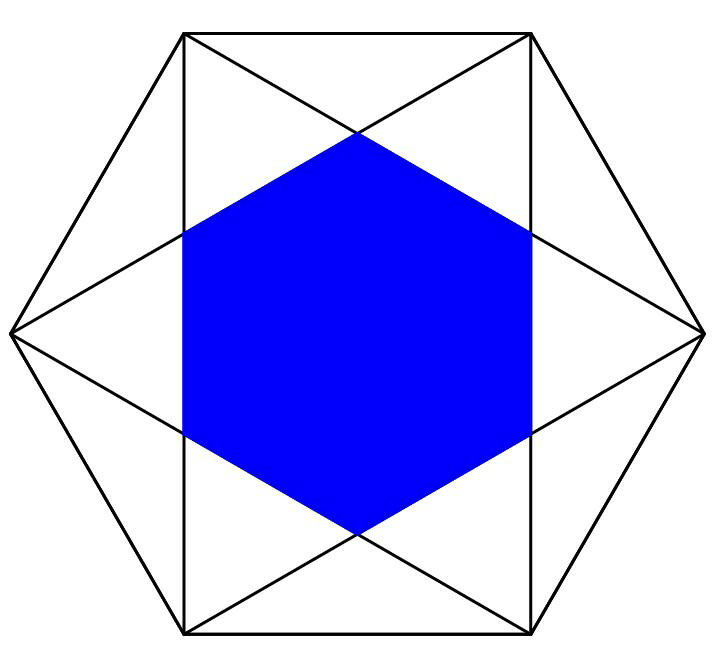
Answered by mrW1 last updated on 26/Jun/17
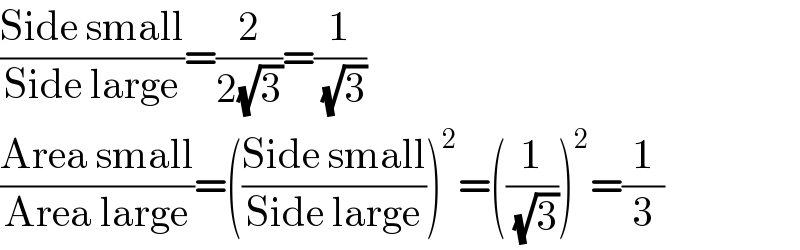
$$\frac{\mathrm{Side}\:\mathrm{small}}{\mathrm{Side}\:\mathrm{large}}=\frac{\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{3}}}=\frac{\mathrm{1}}{\sqrt{\mathrm{3}}} \\ $$$$\frac{\mathrm{Area}\:\mathrm{small}}{\mathrm{Area}\:\mathrm{large}}=\left(\frac{\mathrm{Side}\:\mathrm{small}}{\mathrm{Side}\:\mathrm{large}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Answered by RasheedSoomro last updated on 26/Jun/17
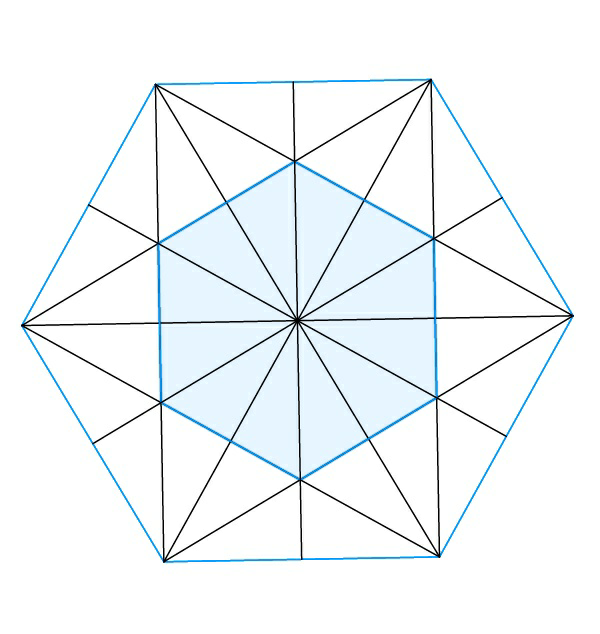
Commented by RasheedSoomro last updated on 26/Jun/17

$$\mathrm{AnOther}\:\mathrm{way} \\ $$$$\frac{\mathrm{Small}\:\mathrm{triangles}\:\mathrm{in}\:\mathrm{inner}\:\mathrm{hexagon}}{\mathrm{Small}\:\mathrm{triangles}\:\mathrm{in}\:\mathrm{outer}\:\mathrm{hexagon}}=\frac{\mathrm{12}}{\mathrm{36}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by Tinkutara last updated on 26/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
