
Question Number 167520 by MikeH last updated on 18/Mar/22
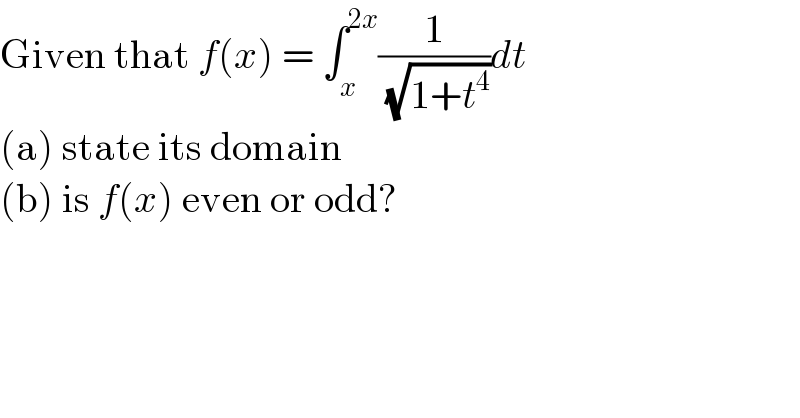
$$\mathrm{Given}\:\mathrm{that}\:{f}\left({x}\right)\:=\:\int_{{x}} ^{\mathrm{2}{x}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{4}} }}{dt} \\ $$$$\left(\mathrm{a}\right)\:\mathrm{state}\:\mathrm{its}\:\mathrm{domain} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{is}\:{f}\left({x}\right)\:\mathrm{even}\:\mathrm{or}\:\mathrm{odd}? \\ $$
Answered by aleks041103 last updated on 18/Mar/22
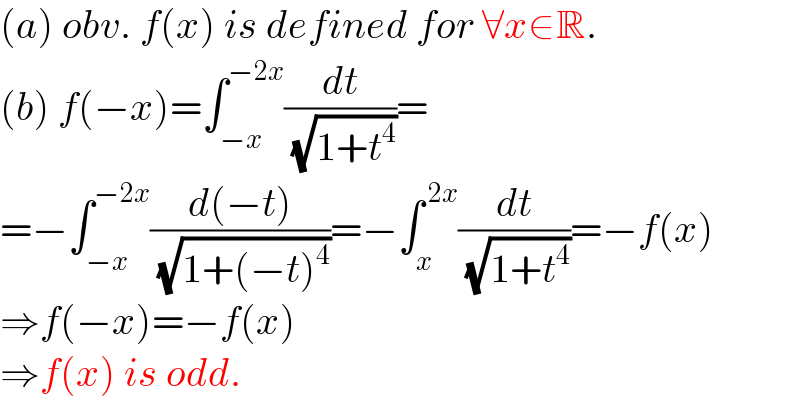
$$\left({a}\right)\:{obv}.\:{f}\left({x}\right)\:{is}\:{defined}\:{for}\:\forall{x}\in\mathbb{R}. \\ $$$$\left({b}\right)\:{f}\left(−{x}\right)=\int_{−{x}} ^{−\mathrm{2}{x}} \frac{{dt}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{4}} }}= \\ $$$$=−\int_{−{x}} ^{−\mathrm{2}{x}} \frac{{d}\left(−{t}\right)}{\:\sqrt{\mathrm{1}+\left(−{t}\right)^{\mathrm{4}} }}=−\int_{{x}} ^{\:\mathrm{2}{x}} \frac{{dt}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{4}} }}=−{f}\left({x}\right) \\ $$$$\Rightarrow{f}\left(−{x}\right)=−{f}\left({x}\right) \\ $$$$\Rightarrow{f}\left({x}\right)\:{is}\:{odd}. \\ $$
