
Question Number 167490 by mathlove last updated on 18/Mar/22
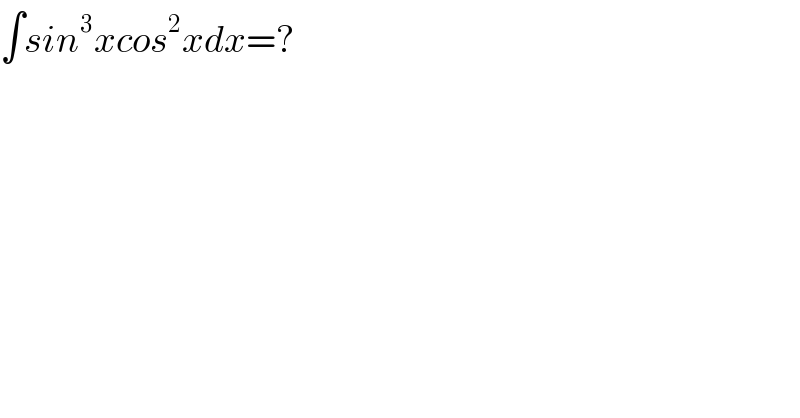
$$\int{sin}^{\mathrm{3}} {xcos}^{\mathrm{2}} {xdx}=? \\ $$
Answered by nimnim last updated on 18/Mar/22
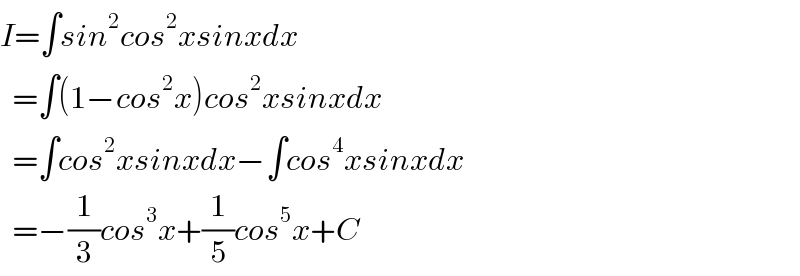
$${I}=\int{sin}^{\mathrm{2}} {cos}^{\mathrm{2}} {xsinxdx} \\ $$$$\:\:=\int\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right){cos}^{\mathrm{2}} {xsinxdx} \\ $$$$\:\:=\int{cos}^{\mathrm{2}} {xsinxdx}−\int{cos}^{\mathrm{4}} {xsinxdx} \\ $$$$\:\:=−\frac{\mathrm{1}}{\mathrm{3}}{cos}^{\mathrm{3}} {x}+\frac{\mathrm{1}}{\mathrm{5}}{cos}^{\mathrm{5}} {x}+{C} \\ $$
