
Question Number 167468 by LEKOUMA last updated on 17/Mar/22
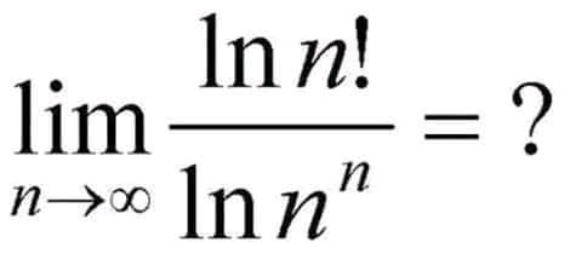
Answered by MJS_new last updated on 17/Mar/22
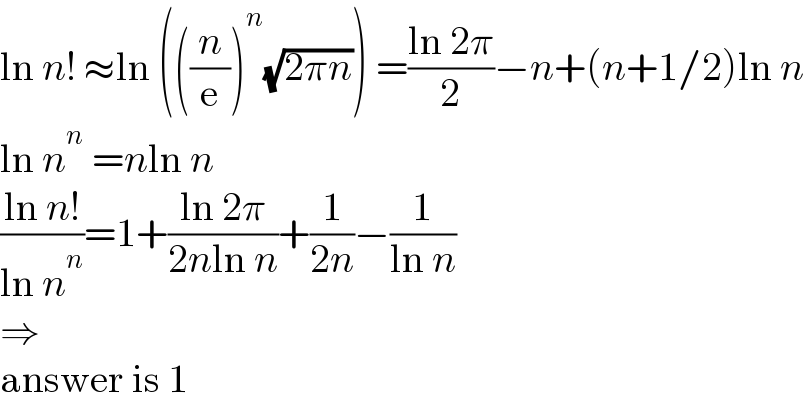
$$\mathrm{ln}\:{n}!\:\approx\mathrm{ln}\:\left(\left(\frac{{n}}{\mathrm{e}}\right)^{{n}} \sqrt{\mathrm{2}\pi{n}}\right)\:=\frac{\mathrm{ln}\:\mathrm{2}\pi}{\mathrm{2}}−{n}+\left({n}+\mathrm{1}/\mathrm{2}\right)\mathrm{ln}\:{n} \\ $$$$\mathrm{ln}\:{n}^{{n}} \:={n}\mathrm{ln}\:{n} \\ $$$$\frac{\mathrm{ln}\:{n}!}{\mathrm{ln}\:{n}^{{n}} }=\mathrm{1}+\frac{\mathrm{ln}\:\mathrm{2}\pi}{\mathrm{2}{n}\mathrm{ln}\:{n}}+\frac{\mathrm{1}}{\mathrm{2}{n}}−\frac{\mathrm{1}}{\mathrm{ln}\:{n}} \\ $$$$\Rightarrow \\ $$$$\mathrm{answer}\:\mathrm{is}\:\mathrm{1} \\ $$
Commented by LEKOUMA last updated on 17/Mar/22

$${Thanks} \\ $$
