
Question Number 167438 by cortano1 last updated on 16/Mar/22
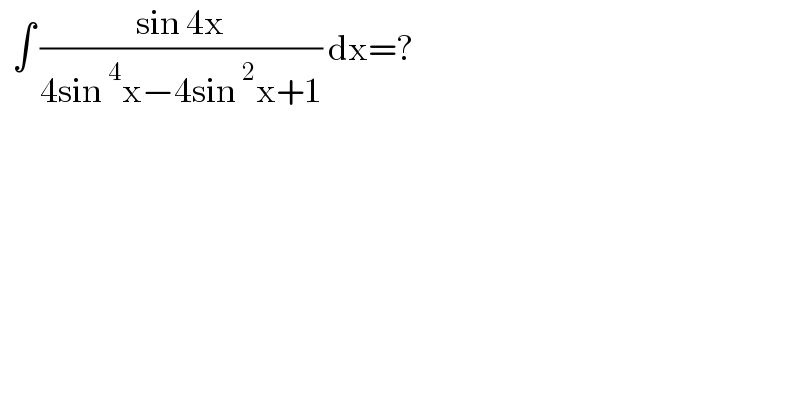
$$\:\:\int\:\frac{\mathrm{sin}\:\mathrm{4x}}{\mathrm{4sin}\:^{\mathrm{4}} \mathrm{x}−\mathrm{4sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{1}}\:\mathrm{dx}=? \\ $$
Answered by MJS_new last updated on 16/Mar/22
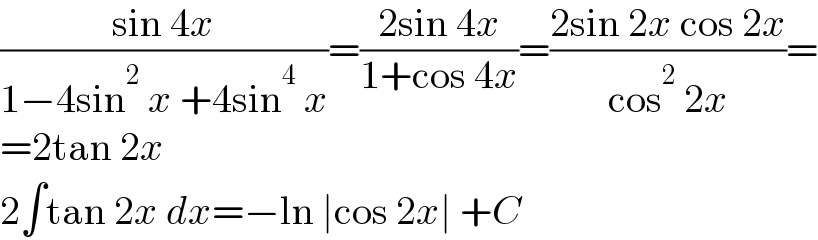
$$\frac{\mathrm{sin}\:\mathrm{4}{x}}{\mathrm{1}−\mathrm{4sin}^{\mathrm{2}} \:{x}\:+\mathrm{4sin}^{\mathrm{4}} \:{x}}=\frac{\mathrm{2sin}\:\mathrm{4}{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{4}{x}}=\frac{\mathrm{2sin}\:\mathrm{2}{x}\:\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}{x}}= \\ $$$$=\mathrm{2tan}\:\mathrm{2}{x} \\ $$$$\mathrm{2}\int\mathrm{tan}\:\mathrm{2}{x}\:{dx}=−\mathrm{ln}\:\mid\mathrm{cos}\:\mathrm{2}{x}\mid\:+{C} \\ $$
Answered by cortano1 last updated on 17/Mar/22
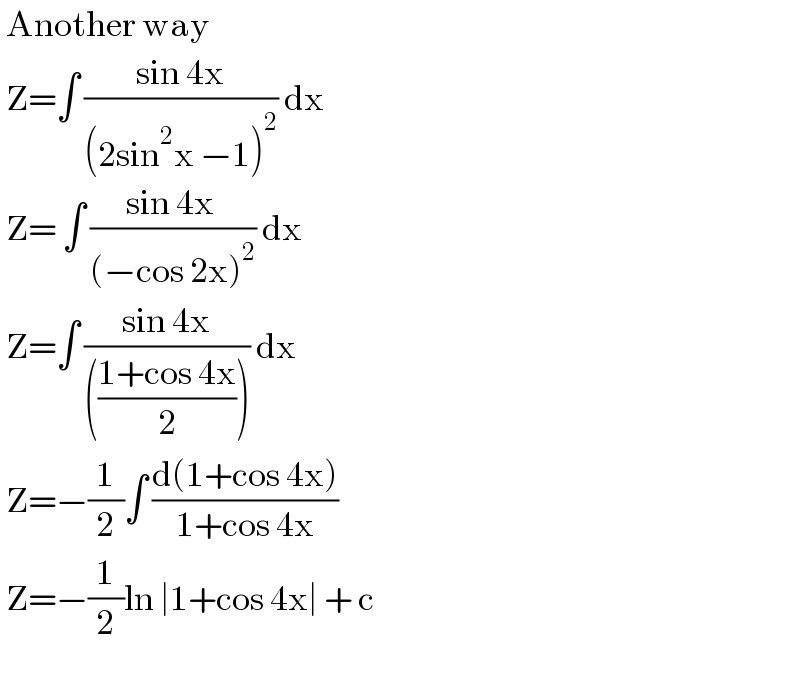
$$\:\mathrm{Another}\:\mathrm{way} \\ $$$$\:\mathrm{Z}=\int\:\frac{\mathrm{sin}\:\mathrm{4x}}{\left(\mathrm{2sin}^{\mathrm{2}} \mathrm{x}\:−\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{dx}\: \\ $$$$\:\mathrm{Z}=\:\int\:\frac{\mathrm{sin}\:\mathrm{4x}\:}{\left(−\mathrm{cos}\:\mathrm{2x}\right)^{\mathrm{2}} }\:\mathrm{dx} \\ $$$$\:\mathrm{Z}=\int\:\frac{\mathrm{sin}\:\mathrm{4x}}{\left(\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{4x}}{\mathrm{2}}\right)}\:\mathrm{dx} \\ $$$$\:\mathrm{Z}=−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{d}\left(\mathrm{1}+\mathrm{cos}\:\mathrm{4x}\right)}{\mathrm{1}+\mathrm{cos}\:\mathrm{4x}} \\ $$$$\:\mathrm{Z}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{1}+\mathrm{cos}\:\mathrm{4x}\mid\:+\:\mathrm{c}\: \\ $$$$ \\ $$
