
Question Number 167434 by greogoury55 last updated on 16/Mar/22
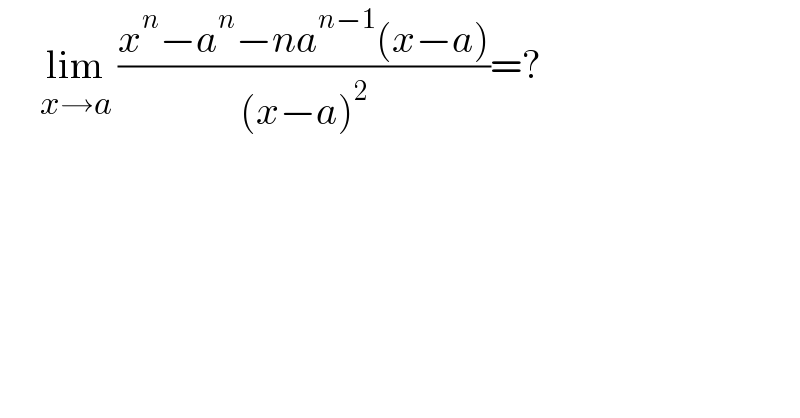
$$\:\:\:\:\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{{x}^{{n}} −{a}^{{n}} −{na}^{{n}−\mathrm{1}} \left({x}−{a}\right)}{\left({x}−{a}\right)^{\mathrm{2}} }=? \\ $$
Answered by qaz last updated on 16/Mar/22
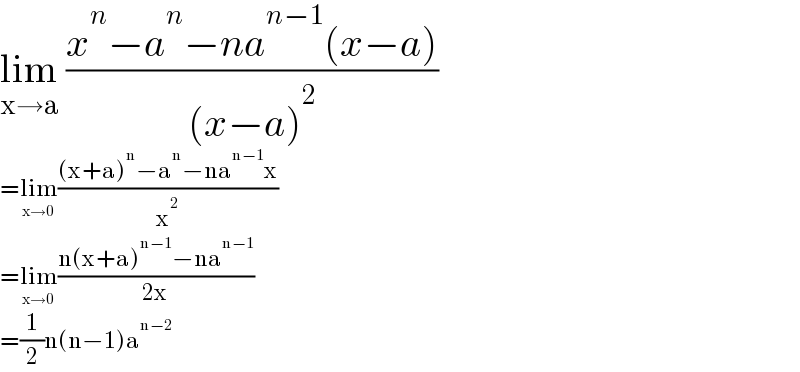
$$\underset{\mathrm{x}\rightarrow\mathrm{a}} {\mathrm{lim}}\:\frac{{x}^{{n}} −{a}^{{n}} −{na}^{{n}−\mathrm{1}} \left({x}−{a}\right)}{\left({x}−{a}\right)^{\mathrm{2}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{x}+\mathrm{a}\right)^{\mathrm{n}} −\mathrm{a}^{\mathrm{n}} −\mathrm{na}^{\mathrm{n}−\mathrm{1}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{n}\left(\mathrm{x}+\mathrm{a}\right)^{\mathrm{n}−\mathrm{1}} −\mathrm{na}^{\mathrm{n}−\mathrm{1}} }{\mathrm{2x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{a}^{\mathrm{n}−\mathrm{2}} \\ $$
Answered by cortano1 last updated on 16/Mar/22
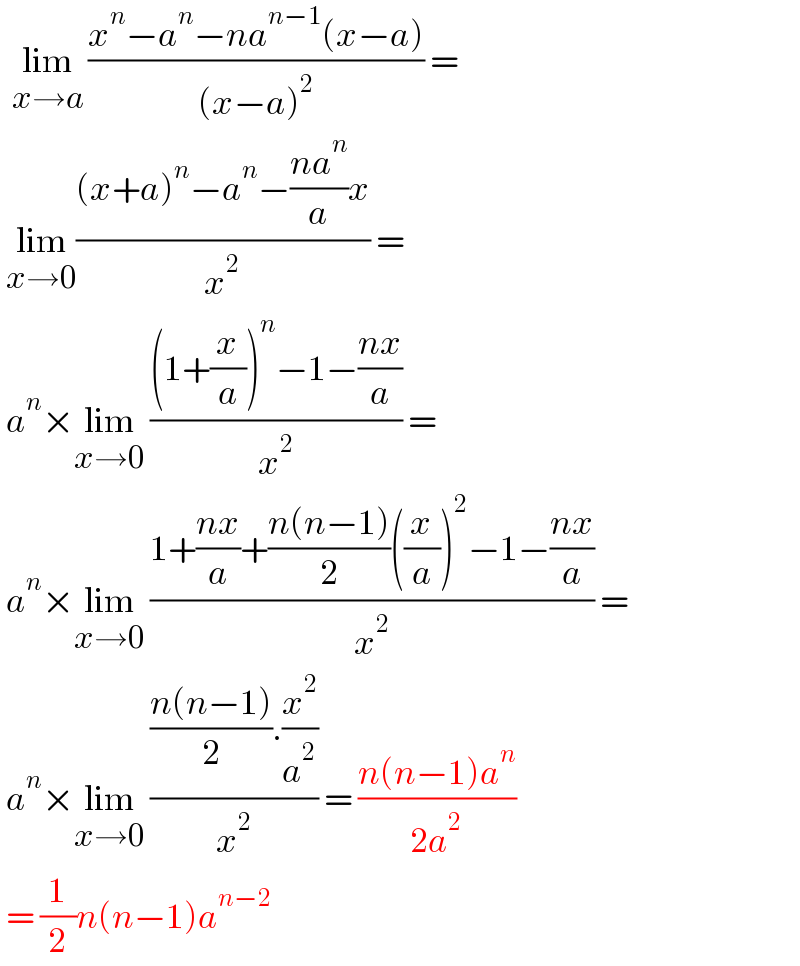
$$\:\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\:\frac{{x}^{{n}} −{a}^{{n}} −{na}^{{n}−\mathrm{1}} \left({x}−{a}\right)}{\left({x}−{a}\right)^{\mathrm{2}} }\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({x}+{a}\right)^{{n}} −{a}^{{n}} −\frac{{na}^{{n}} }{{a}}{x}}{{x}^{\mathrm{2}} }\:= \\ $$$$\:{a}^{{n}} ×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\frac{{x}}{{a}}\right)^{{n}} −\mathrm{1}−\frac{{nx}}{{a}}}{{x}^{\mathrm{2}} }\:= \\ $$$$\:{a}^{{n}} ×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}+\frac{{nx}}{{a}}+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}\left(\frac{{x}}{{a}}\right)^{\mathrm{2}} −\mathrm{1}−\frac{{nx}}{{a}}}{{x}^{\mathrm{2}} }\:= \\ $$$$\:{a}^{{n}} ×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}.\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}{{x}^{\mathrm{2}} }\:=\:\frac{{n}\left({n}−\mathrm{1}\right){a}^{{n}} }{\mathrm{2}{a}^{\mathrm{2}} } \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}{n}\left({n}−\mathrm{1}\right){a}^{{n}−\mathrm{2}} \: \\ $$
Commented by greogoury55 last updated on 18/Mar/22

$${nice} \\ $$
