
Question Number 167372 by LEKOUMA last updated on 14/Mar/22
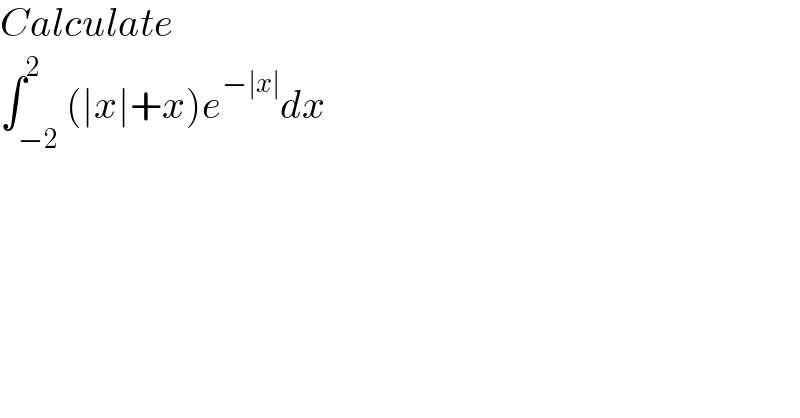
$${Calculate}\: \\ $$$$\int_{−\mathrm{2}} ^{\mathrm{2}} \left(\mid{x}\mid+{x}\right){e}^{−\mid{x}\mid} {dx} \\ $$
Answered by Mathspace last updated on 14/Mar/22
![I=∫_(−2) ^2 ∣x∣e^(−∣x∣) dx(→paire) +∫_(−2) ^2 xe^(−∣x∣) dx(→impaire) =2∫_0 ^2 xe^(−x) dx +o =2{ [−xe^(−x) ]_0 ^2 −∫_0 ^2 (−e^(−x) )dx} =2{−2e^(−2) +[−e^(−x) ]_0 ^2 } =2{−2e^(−2) +1−e^(−2) } =2{−3e^(−2) +1}=2−(6/e^2 )](Q167377.png)
$${I}=\int_{−\mathrm{2}} ^{\mathrm{2}} \mid{x}\mid{e}^{−\mid{x}\mid} {dx}\left(\rightarrow{paire}\right) \\ $$$$+\int_{−\mathrm{2}} ^{\mathrm{2}} {xe}^{−\mid{x}\mid} {dx}\left(\rightarrow{impaire}\right) \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}} {xe}^{−{x}} {dx}\:+{o} \\ $$$$=\mathrm{2}\left\{\:\:\left[−{xe}^{−{x}} \right]_{\mathrm{0}} ^{\mathrm{2}} −\int_{\mathrm{0}} ^{\mathrm{2}} \left(−{e}^{−{x}} \right){dx}\right\} \\ $$$$=\mathrm{2}\left\{−\mathrm{2}{e}^{−\mathrm{2}} +\left[−{e}^{−{x}} \right]_{\mathrm{0}} ^{\mathrm{2}} \right\} \\ $$$$=\mathrm{2}\left\{−\mathrm{2}{e}^{−\mathrm{2}} +\mathrm{1}−{e}^{−\mathrm{2}} \right\} \\ $$$$=\mathrm{2}\left\{−\mathrm{3}{e}^{−\mathrm{2}} +\mathrm{1}\right\}=\mathrm{2}−\frac{\mathrm{6}}{{e}^{\mathrm{2}} } \\ $$
Commented by LEKOUMA last updated on 15/Mar/22

$${Thanks} \\ $$
