
Question Number 167200 by Tawa11 last updated on 09/Mar/22

Answered by mr W last updated on 09/Mar/22
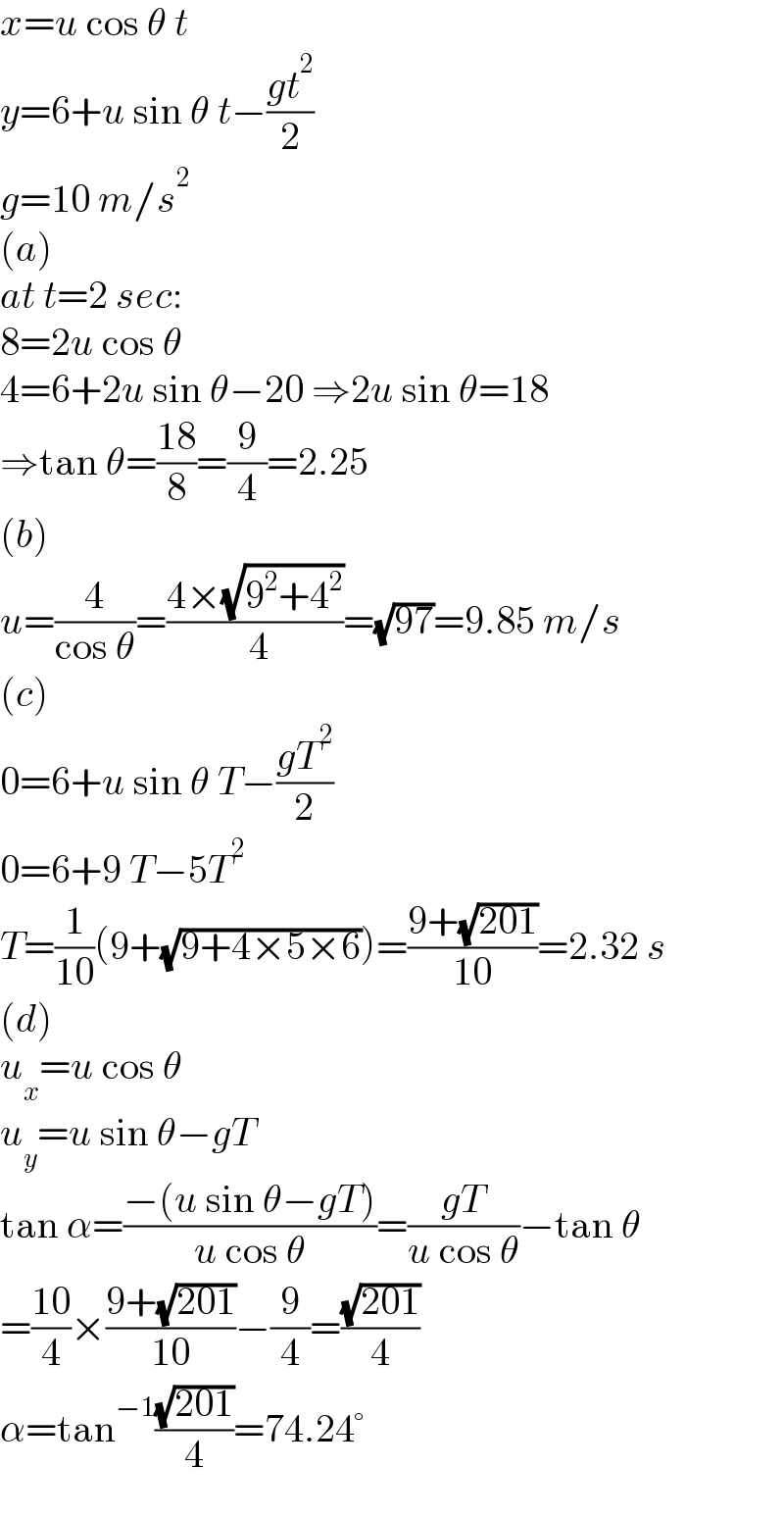
$${x}={u}\:\mathrm{cos}\:\theta\:{t} \\ $$$${y}=\mathrm{6}+{u}\:\mathrm{sin}\:\theta\:{t}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${g}=\mathrm{10}\:{m}/{s}^{\mathrm{2}} \\ $$$$\left({a}\right) \\ $$$${at}\:{t}=\mathrm{2}\:{sec}: \\ $$$$\mathrm{8}=\mathrm{2}{u}\:\mathrm{cos}\:\theta \\ $$$$\mathrm{4}=\mathrm{6}+\mathrm{2}{u}\:\mathrm{sin}\:\theta−\mathrm{20}\:\Rightarrow\mathrm{2}{u}\:\mathrm{sin}\:\theta=\mathrm{18} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{18}}{\mathrm{8}}=\frac{\mathrm{9}}{\mathrm{4}}=\mathrm{2}.\mathrm{25} \\ $$$$\left({b}\right) \\ $$$${u}=\frac{\mathrm{4}}{\mathrm{cos}\:\theta}=\frac{\mathrm{4}×\sqrt{\mathrm{9}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} }}{\:\mathrm{4}}=\sqrt{\mathrm{97}}=\mathrm{9}.\mathrm{85}\:{m}/{s} \\ $$$$\left({c}\right) \\ $$$$\mathrm{0}=\mathrm{6}+{u}\:\mathrm{sin}\:\theta\:{T}−\frac{{gT}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{0}=\mathrm{6}+\mathrm{9}\:{T}−\mathrm{5}{T}^{\mathrm{2}} \\ $$$${T}=\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{9}+\sqrt{\mathrm{9}+\mathrm{4}×\mathrm{5}×\mathrm{6}}\right)=\frac{\mathrm{9}+\sqrt{\mathrm{201}}}{\mathrm{10}}=\mathrm{2}.\mathrm{32}\:{s} \\ $$$$\left({d}\right) \\ $$$${u}_{{x}} ={u}\:\mathrm{cos}\:\theta \\ $$$${u}_{{y}} ={u}\:\mathrm{sin}\:\theta−{gT} \\ $$$$\mathrm{tan}\:\alpha=\frac{−\left({u}\:\mathrm{sin}\:\theta−{gT}\right)}{{u}\:\mathrm{cos}\:\theta}=\frac{{gT}}{{u}\:\mathrm{cos}\:\theta}−\mathrm{tan}\:\theta \\ $$$$=\frac{\mathrm{10}}{\mathrm{4}}×\frac{\mathrm{9}+\sqrt{\mathrm{201}}}{\mathrm{10}}−\frac{\mathrm{9}}{\mathrm{4}}=\frac{\sqrt{\mathrm{201}}}{\mathrm{4}} \\ $$$$\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{201}}}{\mathrm{4}}=\mathrm{74}.\mathrm{24}° \\ $$
Commented by Tawa11 last updated on 09/Mar/22
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
