
Question Number 167120 by DAVONG last updated on 07/Mar/22
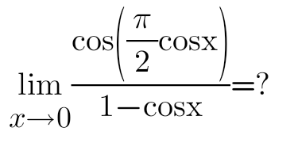
Answered by TheSupreme last updated on 07/Mar/22
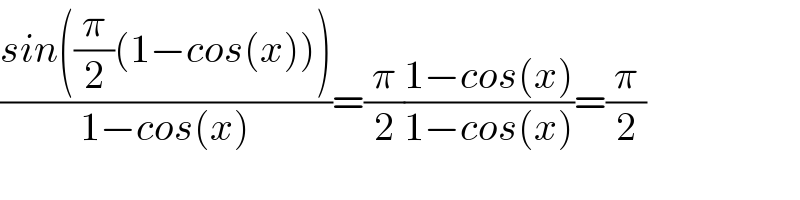
$$\frac{{sin}\left(\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−{cos}\left({x}\right)\right)\right)}{\mathrm{1}−{cos}\left({x}\right)}=\frac{\pi}{\mathrm{2}}\frac{\mathrm{1}−{cos}\left({x}\right)}{\mathrm{1}−{cos}\left({x}\right)}=\frac{\pi}{\mathrm{2}} \\ $$
Answered by Mathspace last updated on 07/Mar/22
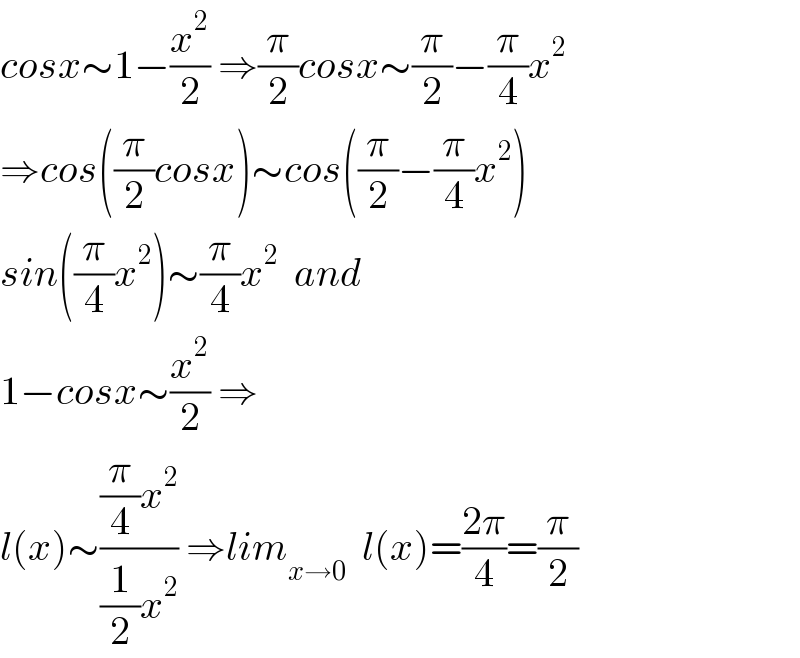
$${cosx}\sim\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\frac{\pi}{\mathrm{2}}{cosx}\sim\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}{x}^{\mathrm{2}} \\ $$$$\Rightarrow{cos}\left(\frac{\pi}{\mathrm{2}}{cosx}\right)\sim{cos}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}{x}^{\mathrm{2}} \right) \\ $$$${sin}\left(\frac{\pi}{\mathrm{4}}{x}^{\mathrm{2}} \right)\sim\frac{\pi}{\mathrm{4}}{x}^{\mathrm{2}} \:\:{and} \\ $$$$\mathrm{1}−{cosx}\sim\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$${l}\left({x}\right)\sim\frac{\frac{\pi}{\mathrm{4}}{x}^{\mathrm{2}} }{\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} }\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:{l}\left({x}\right)=\frac{\mathrm{2}\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{2}} \\ $$
Answered by kapoorshah last updated on 07/Mar/22
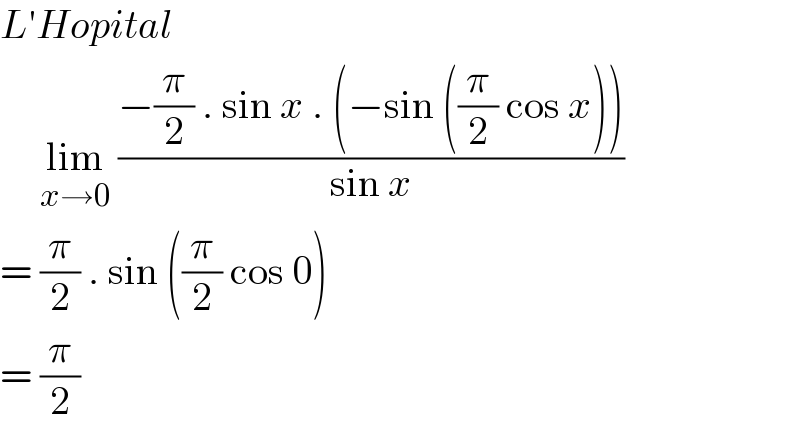
$${L}'{Hopital} \\ $$$$\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\frac{\pi}{\mathrm{2}}\:.\:\mathrm{sin}\:{x}\:.\:\left(−\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}\:\mathrm{cos}\:{x}\right)\right)}{\mathrm{sin}\:{x}} \\ $$$$=\:\frac{\pi}{\mathrm{2}}\:.\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}\:\mathrm{cos}\:\mathrm{0}\right) \\ $$$$=\:\frac{\pi}{\mathrm{2}} \\ $$
