
Question Number 167100 by qaz last updated on 06/Mar/22
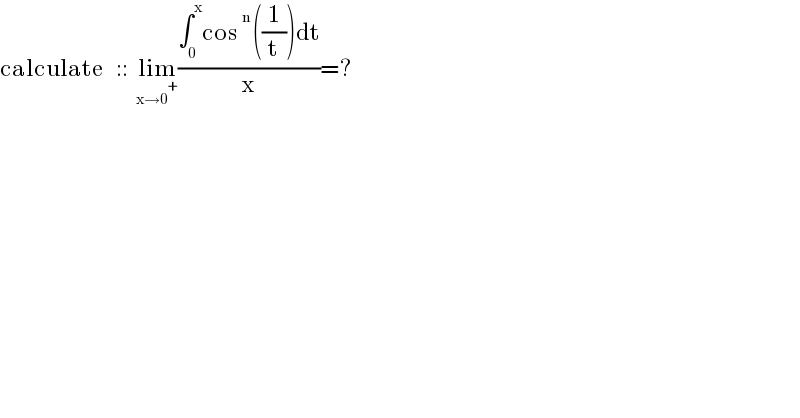
$$\mathrm{calculate}\:\:\:::\:\:\underset{\mathrm{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\int_{\mathrm{0}} ^{\mathrm{x}} \mathrm{cos}\:^{\mathrm{n}} \left(\frac{\mathrm{1}}{\mathrm{t}}\right)\mathrm{dt}}{\mathrm{x}}=? \\ $$
Commented by mindispower last updated on 09/Mar/22

$${i}\:{deleat}\:{my}\:{solution}\:{i}\:{see}\:{my}\:{error} \\ $$$${i}\:{wil}\left[{post}\:{a}\:{solution}\:{later}\right. \\ $$$${Thanx}\:{sir}\: \\ $$
Answered by Mathspace last updated on 07/Mar/22
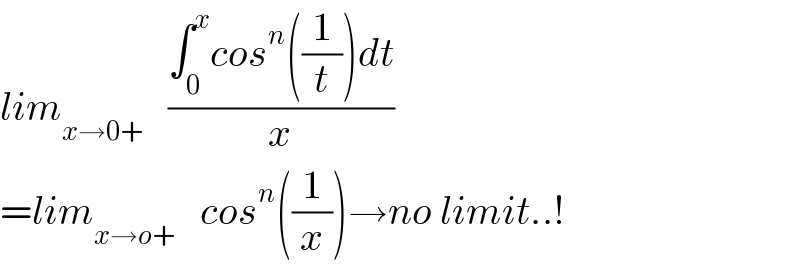
$${lim}_{{x}\rightarrow\mathrm{0}+} \:\:\:\frac{\int_{\mathrm{0}} ^{{x}} {cos}^{{n}} \left(\frac{\mathrm{1}}{{t}}\right){dt}}{{x}} \\ $$$$={lim}_{{x}\rightarrow{o}+} \:\:\:{cos}^{{n}} \left(\frac{\mathrm{1}}{{x}}\right)\rightarrow{no}\:{limit}..! \\ $$
