
Question Number 167009 by mnjuly1970 last updated on 04/Mar/22
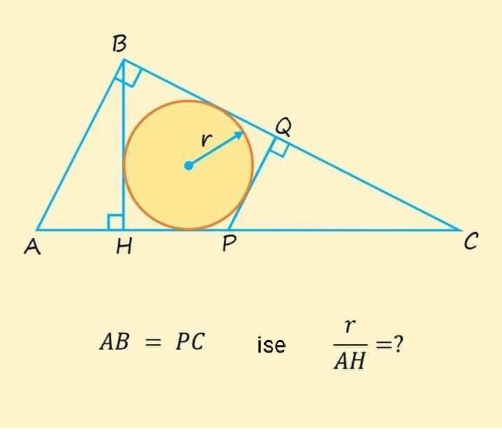
Answered by mr W last updated on 04/Mar/22
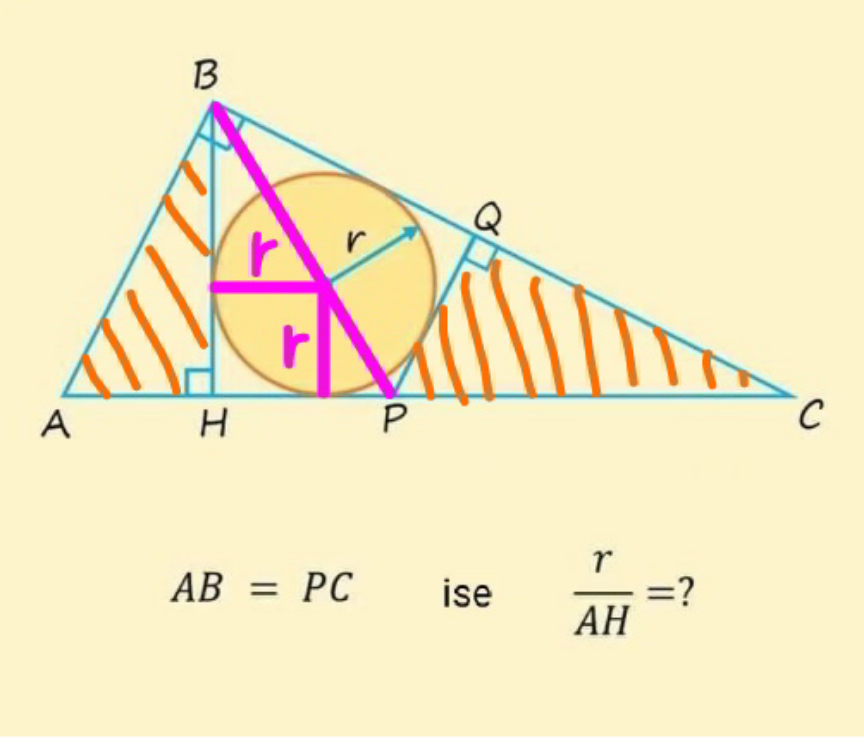
Commented by mr W last updated on 04/Mar/22
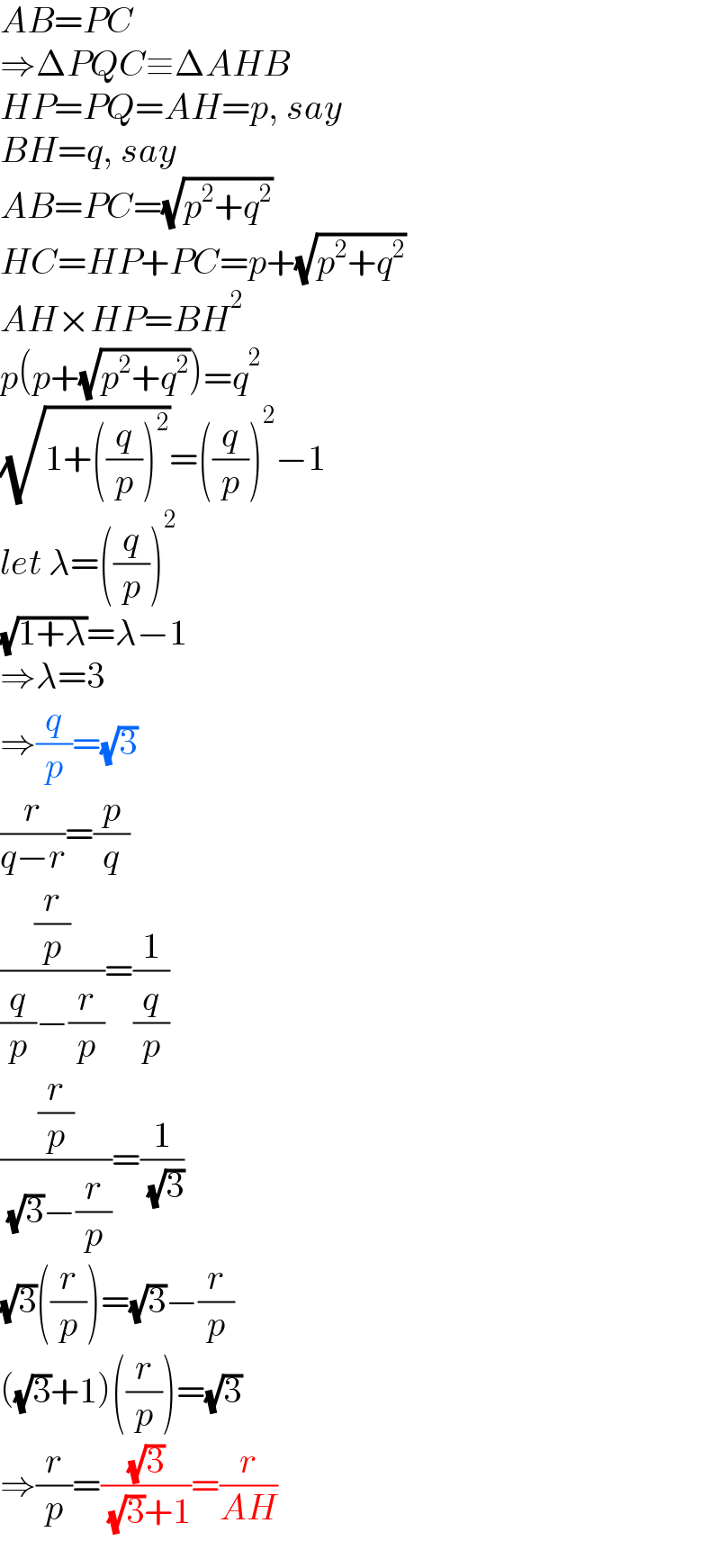
$${AB}={PC} \\ $$$$\Rightarrow\Delta{PQC}\equiv\Delta{AHB} \\ $$$${HP}={PQ}={AH}={p},\:{say} \\ $$$${BH}={q},\:{say} \\ $$$${AB}={PC}=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} } \\ $$$${HC}={HP}+{PC}={p}+\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} } \\ $$$${AH}×{HP}={BH}^{\mathrm{2}} \\ $$$${p}\left({p}+\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }\right)={q}^{\mathrm{2}} \\ $$$$\sqrt{\mathrm{1}+\left(\frac{{q}}{{p}}\right)^{\mathrm{2}} }=\left(\frac{{q}}{{p}}\right)^{\mathrm{2}} −\mathrm{1} \\ $$$${let}\:\lambda=\left(\frac{{q}}{{p}}\right)^{\mathrm{2}} \\ $$$$\sqrt{\mathrm{1}+\lambda}=\lambda−\mathrm{1} \\ $$$$\Rightarrow\lambda=\mathrm{3} \\ $$$$\Rightarrow\frac{{q}}{{p}}=\sqrt{\mathrm{3}} \\ $$$$\frac{{r}}{{q}−{r}}=\frac{{p}}{{q}} \\ $$$$\frac{\frac{{r}}{{p}}}{\frac{{q}}{{p}}−\frac{{r}}{{p}}}=\frac{\mathrm{1}}{\frac{{q}}{{p}}} \\ $$$$\frac{\frac{{r}}{{p}}}{\:\sqrt{\mathrm{3}}−\frac{{r}}{{p}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\sqrt{\mathrm{3}}\left(\frac{{r}}{{p}}\right)=\sqrt{\mathrm{3}}−\frac{{r}}{{p}} \\ $$$$\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)\left(\frac{{r}}{{p}}\right)=\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\frac{{r}}{{p}}=\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{3}}+\mathrm{1}}=\frac{{r}}{{AH}} \\ $$
Commented by mnjuly1970 last updated on 05/Mar/22
$$\:\:\:{thanks}\:{alot}\:{sir}\:{W} \\ $$
Commented by Tawa11 last updated on 05/Mar/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
