
Question Number 166939 by cortano1 last updated on 03/Mar/22

Answered by som(math1967) last updated on 03/Mar/22
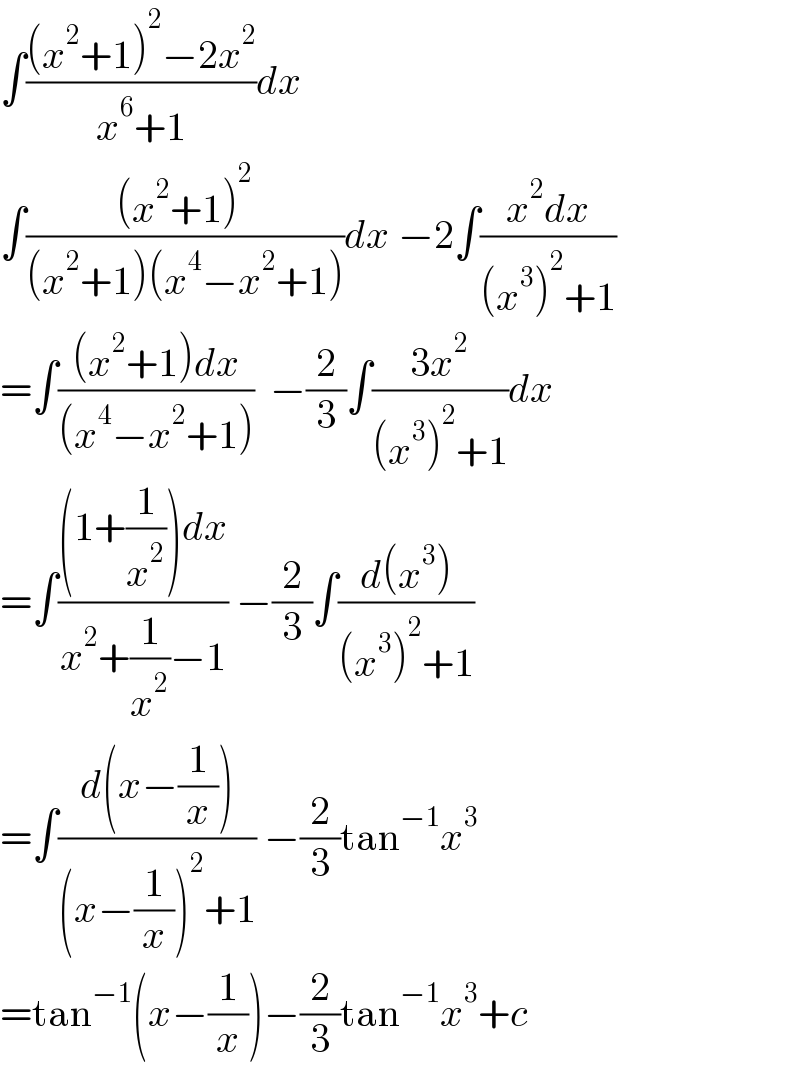
$$\int\frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}} }{{x}^{\mathrm{6}} +\mathrm{1}}{dx} \\ $$$$\int\frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)}{dx}\:−\mathrm{2}\int\frac{{x}^{\mathrm{2}} {dx}}{\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\int\frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right){dx}}{\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)}\:\:−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{3}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$=\int\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){dx}}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{1}}\:−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{d}\left({x}^{\mathrm{3}} \right)}{\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{1}}\:−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} {x}^{\mathrm{3}} \\ $$$$=\mathrm{tan}^{−\mathrm{1}} \left({x}−\frac{\mathrm{1}}{{x}}\right)−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} {x}^{\mathrm{3}} +{c} \\ $$
Commented by MJS_new last updated on 03/Mar/22
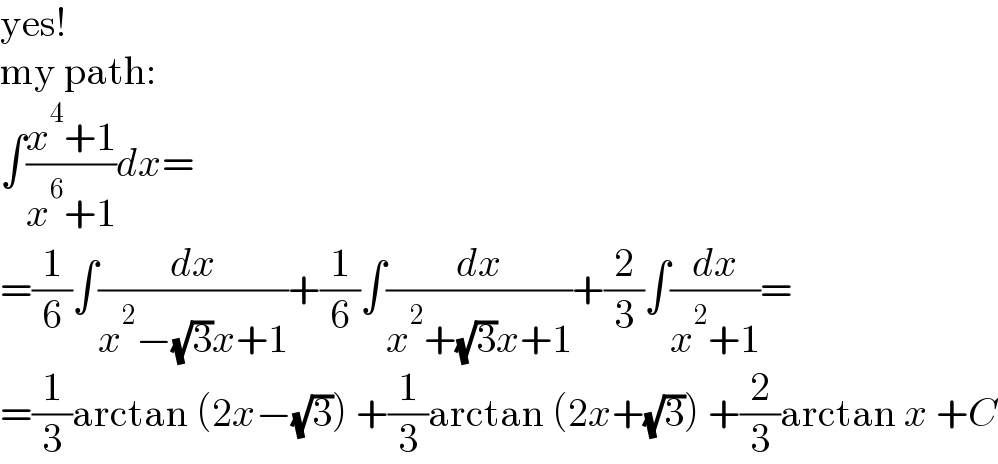
$$\mathrm{yes}! \\ $$$$\mathrm{my}\:\mathrm{path}: \\ $$$$\int\frac{{x}^{\mathrm{4}} +\mathrm{1}}{{x}^{\mathrm{6}} +\mathrm{1}}{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{dx}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}+\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arctan}\:\left(\mathrm{2}{x}−\sqrt{\mathrm{3}}\right)\:+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arctan}\:\left(\mathrm{2}{x}+\sqrt{\mathrm{3}}\right)\:+\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arctan}\:{x}\:+{C} \\ $$
Commented by som(math1967) last updated on 04/Mar/22

$${nice}\:{path}\:{sir} \\ $$
Commented by MJS_new last updated on 04/Mar/22
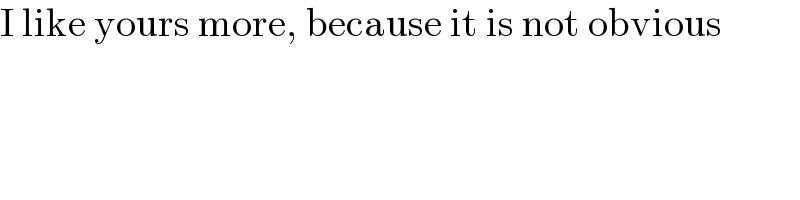
$$\mathrm{I}\:\mathrm{like}\:\mathrm{yours}\:\mathrm{more},\:\mathrm{because}\:\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{obvious} \\ $$
