
Question Number 16685 by rish@bh last updated on 25/Jun/17

$$\mathrm{If}\:\mathrm{cos}\:\left(\theta−\alpha\right),\mathrm{cos}\:\theta\:\mathrm{and}\:\mathrm{cos}\:\left(\theta+\alpha\right) \\ $$$$\:\mathrm{are}\:\mathrm{in}\:\mathrm{HP},\:\mathrm{then} \\ $$$$\mathrm{cos}\:\theta\mathrm{sec}\:\frac{\alpha}{\mathrm{2}}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\left.\mathrm{a}\right)\pm\sqrt{\mathrm{2}} \\ $$$$\left.{b}\right)\:\pm\sqrt{\mathrm{3}} \\ $$$$\left.{c}\right)\pm\frac{\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$$$\left.{d}\right)\mathrm{None}\:\mathrm{of}\:\mathrm{these} \\ $$
Answered by sushmitak last updated on 25/Jun/17
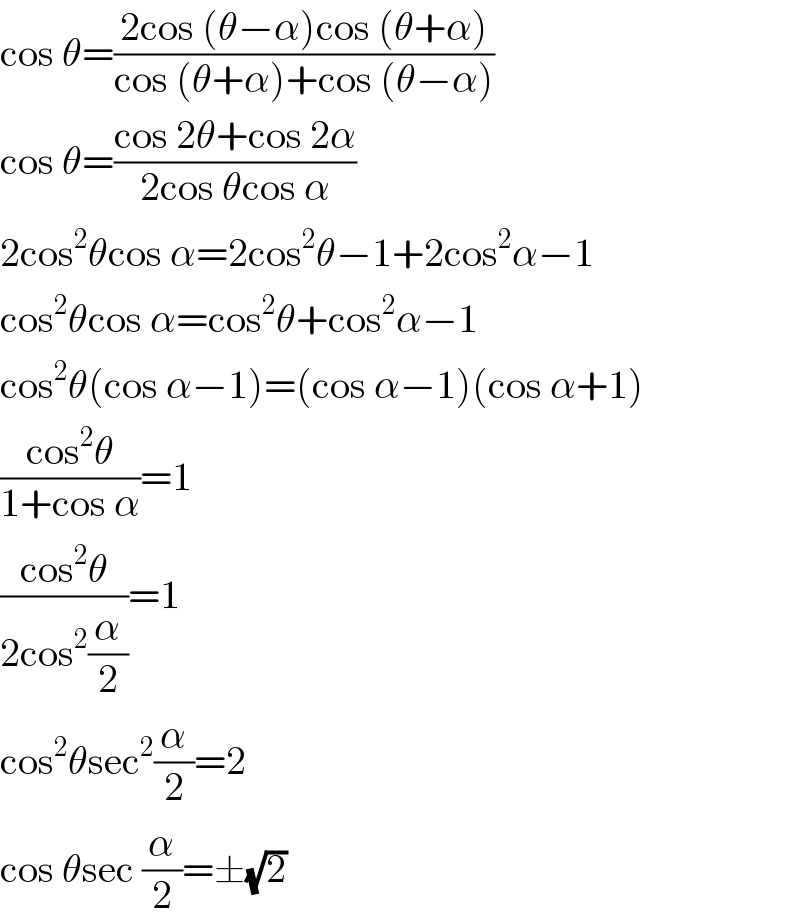
$$\mathrm{cos}\:\theta=\frac{\mathrm{2cos}\:\left(\theta−\alpha\right)\mathrm{cos}\:\left(\theta+\alpha\right)}{\mathrm{cos}\:\left(\theta+\alpha\right)+\mathrm{cos}\:\left(\theta−\alpha\right)} \\ $$$$\mathrm{cos}\:\theta=\frac{\mathrm{cos}\:\mathrm{2}\theta+\mathrm{cos}\:\mathrm{2}\alpha}{\mathrm{2cos}\:\theta\mathrm{cos}\:\alpha} \\ $$$$\mathrm{2cos}^{\mathrm{2}} \theta\mathrm{cos}\:\alpha=\mathrm{2cos}^{\mathrm{2}} \theta−\mathrm{1}+\mathrm{2cos}^{\mathrm{2}} \alpha−\mathrm{1} \\ $$$$\mathrm{cos}^{\mathrm{2}} \theta\mathrm{cos}\:\alpha=\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{cos}^{\mathrm{2}} \alpha−\mathrm{1} \\ $$$$\mathrm{cos}^{\mathrm{2}} \theta\left(\mathrm{cos}\:\alpha−\mathrm{1}\right)=\left(\mathrm{cos}\:\alpha−\mathrm{1}\right)\left(\mathrm{cos}\:\alpha+\mathrm{1}\right) \\ $$$$\frac{\mathrm{cos}^{\mathrm{2}} \theta}{\mathrm{1}+\mathrm{cos}\:\alpha}=\mathrm{1} \\ $$$$\frac{\mathrm{cos}^{\mathrm{2}} \theta}{\mathrm{2cos}^{\mathrm{2}} \frac{\alpha}{\mathrm{2}}}=\mathrm{1} \\ $$$$\mathrm{cos}^{\mathrm{2}} \theta\mathrm{sec}^{\mathrm{2}} \frac{\alpha}{\mathrm{2}}=\mathrm{2} \\ $$$$\mathrm{cos}\:\theta\mathrm{sec}\:\frac{\alpha}{\mathrm{2}}=\pm\sqrt{\mathrm{2}} \\ $$
