
Previous in Relation and Functions Next in Relation and Functions
Question Number 1668 by 123456 last updated on 30/Aug/15
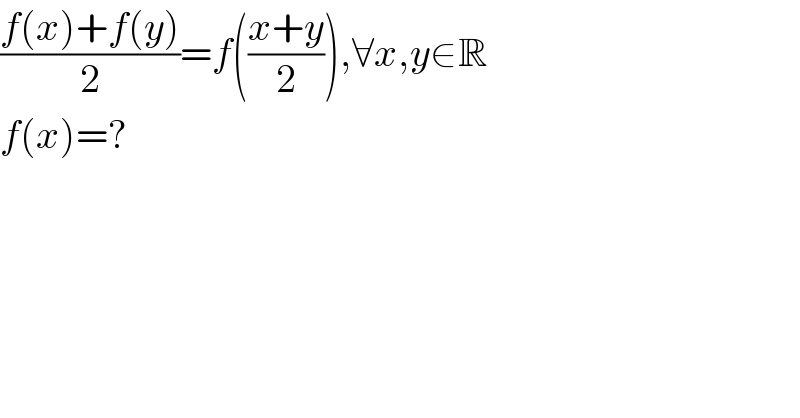
$$\frac{{f}\left({x}\right)+{f}\left({y}\right)}{\mathrm{2}}={f}\left(\frac{{x}+{y}}{\mathrm{2}}\right),\forall{x},{y}\in\mathbb{R} \\ $$$${f}\left({x}\right)=? \\ $$
Commented by Rasheed Ahmad last updated on 30/Aug/15
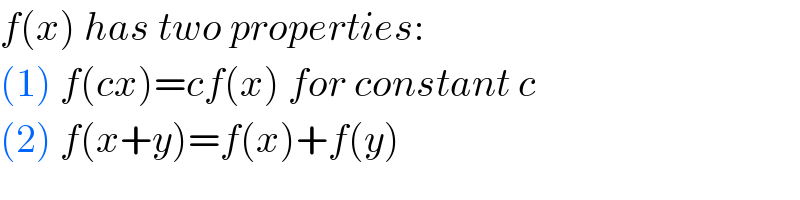
$${f}\left({x}\right)\:{has}\:{two}\:{properties}: \\ $$$$\left(\mathrm{1}\right)\:{f}\left({cx}\right)={cf}\left({x}\right)\:{for}\:{constant}\:{c} \\ $$$$\left(\mathrm{2}\right)\:{f}\left({x}+{y}\right)={f}\left({x}\right)+{f}\left({y}\right) \\ $$
Answered by prakash jain last updated on 02/Sep/15

$${f}\left({x}\right)={kx} \\ $$
