
Question Number 166633 by mathlove last updated on 23/Feb/22
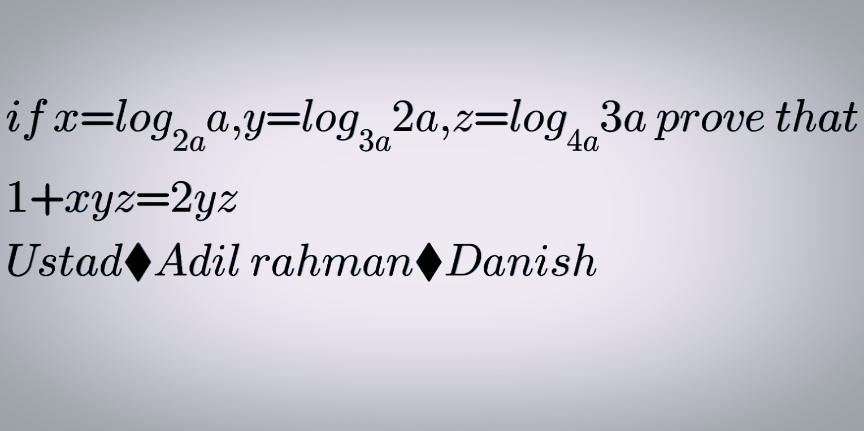
Answered by mahdipoor last updated on 23/Feb/22
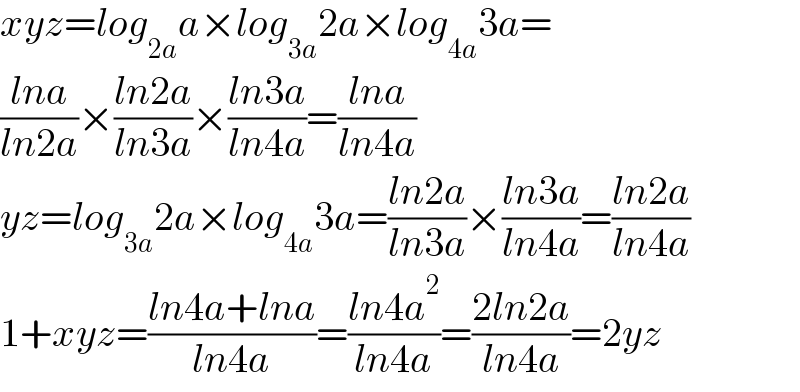
$${xyz}={log}_{\mathrm{2}{a}} {a}×{log}_{\mathrm{3}{a}} \mathrm{2}{a}×{log}_{\mathrm{4}{a}} \mathrm{3}{a}= \\ $$$$\frac{{lna}}{{ln}\mathrm{2}{a}}×\frac{{ln}\mathrm{2}{a}}{{ln}\mathrm{3}{a}}×\frac{{ln}\mathrm{3}{a}}{{ln}\mathrm{4}{a}}=\frac{{lna}}{{ln}\mathrm{4}{a}} \\ $$$${yz}={log}_{\mathrm{3}{a}} \mathrm{2}{a}×{log}_{\mathrm{4}{a}} \mathrm{3}{a}=\frac{{ln}\mathrm{2}{a}}{{ln}\mathrm{3}{a}}×\frac{{ln}\mathrm{3}{a}}{{ln}\mathrm{4}{a}}=\frac{{ln}\mathrm{2}{a}}{{ln}\mathrm{4}{a}} \\ $$$$\mathrm{1}+{xyz}=\frac{{ln}\mathrm{4}{a}+{lna}}{{ln}\mathrm{4}{a}}=\frac{{ln}\mathrm{4}{a}^{\mathrm{2}} }{{ln}\mathrm{4}{a}}=\frac{\mathrm{2}{ln}\mathrm{2}{a}}{{ln}\mathrm{4}{a}}=\mathrm{2}{yz} \\ $$
