
Question Number 166619 by BagusSetyoWibowo last updated on 23/Feb/22
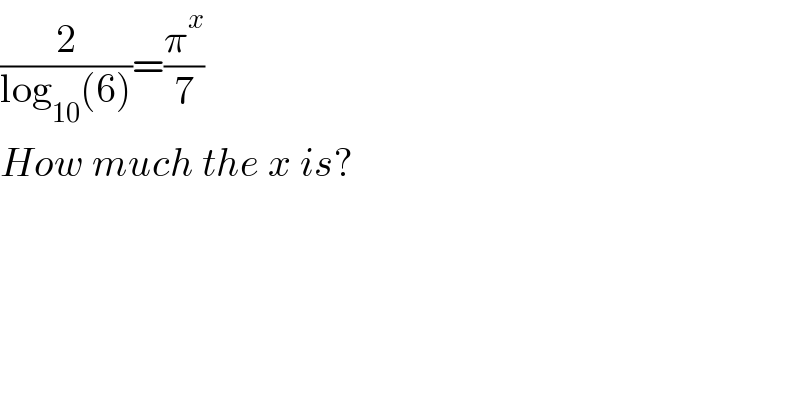
$$\frac{\mathrm{2}}{\mathrm{log}_{\mathrm{10}} \left(\mathrm{6}\right)}=\frac{\pi^{{x}} }{\mathrm{7}} \\ $$$${How}\:{much}\:{the}\:{x}\:{is}? \\ $$
Answered by TheSupreme last updated on 23/Feb/22
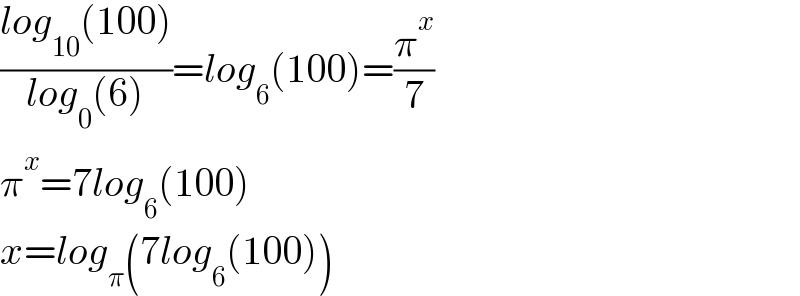
$$\frac{{log}_{\mathrm{10}} \left(\mathrm{100}\right)}{{log}_{\mathrm{0}} \left(\mathrm{6}\right)}={log}_{\mathrm{6}} \left(\mathrm{100}\right)=\frac{\pi^{{x}} }{\mathrm{7}} \\ $$$$\pi^{{x}} =\mathrm{7}{log}_{\mathrm{6}} \left(\mathrm{100}\right) \\ $$$${x}={log}_{\pi} \left(\mathrm{7}{log}_{\mathrm{6}} \left(\mathrm{100}\right)\right) \\ $$
Commented by BagusSetyoWibowo last updated on 24/Feb/22
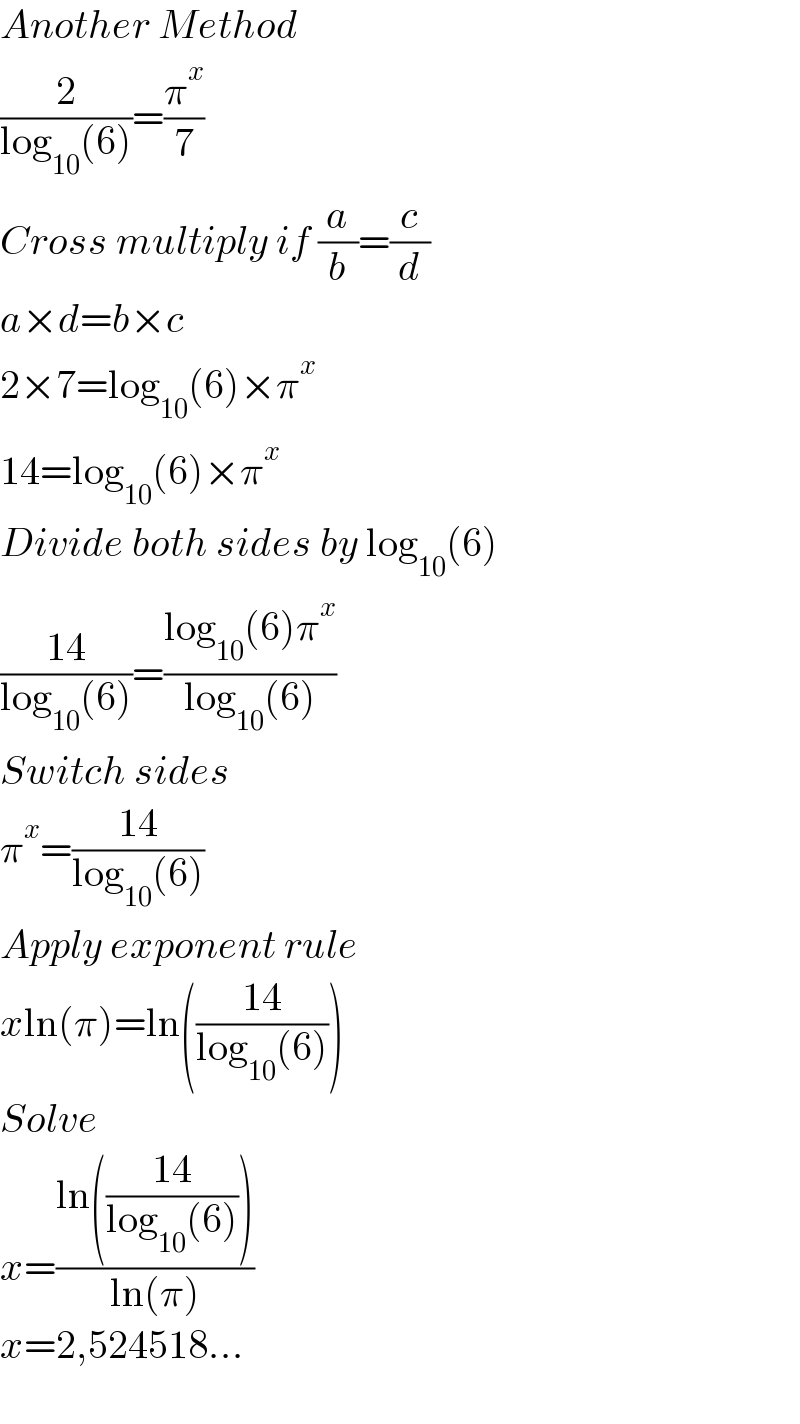
$${Another}\:{Method} \\ $$$$\frac{\mathrm{2}}{\mathrm{log}_{\mathrm{10}} \left(\mathrm{6}\right)}=\frac{\pi^{{x}} }{\mathrm{7}} \\ $$$${Cross}\:{multiply}\:{if}\:\frac{{a}}{{b}}=\frac{{c}}{{d}} \\ $$$${a}×{d}={b}×{c} \\ $$$$\mathrm{2}×\mathrm{7}=\mathrm{log}_{\mathrm{10}} \left(\mathrm{6}\right)×\pi^{{x}} \\ $$$$\mathrm{14}=\mathrm{log}_{\mathrm{10}} \left(\mathrm{6}\right)×\pi^{{x}} \\ $$$${Divide}\:{both}\:{sides}\:{by}\:\mathrm{log}_{\mathrm{10}} \left(\mathrm{6}\right) \\ $$$$\frac{\mathrm{14}}{\mathrm{log}_{\mathrm{10}} \left(\mathrm{6}\right)}=\frac{\mathrm{log}_{\mathrm{10}} \left(\mathrm{6}\right)\pi^{{x}} }{\mathrm{log}_{\mathrm{10}} \left(\mathrm{6}\right)} \\ $$$${Switch}\:{sides} \\ $$$$\pi^{{x}} =\frac{\mathrm{14}}{\mathrm{log}_{\mathrm{10}} \left(\mathrm{6}\right)} \\ $$$${Apply}\:{exponent}\:{rule} \\ $$$${x}\mathrm{ln}\left(\pi\right)=\mathrm{ln}\left(\frac{\mathrm{14}}{\mathrm{log}_{\mathrm{10}} \left(\mathrm{6}\right)}\right) \\ $$$${Solve} \\ $$$${x}=\frac{\mathrm{ln}\left(\frac{\mathrm{14}}{\mathrm{log}_{\mathrm{10}} \left(\mathrm{6}\right)}\right)}{\mathrm{ln}\left(\pi\right)} \\ $$$${x}=\mathrm{2},\mathrm{524518}... \\ $$$$ \\ $$
