
Question Number 166257 by mnjuly1970 last updated on 16/Feb/22
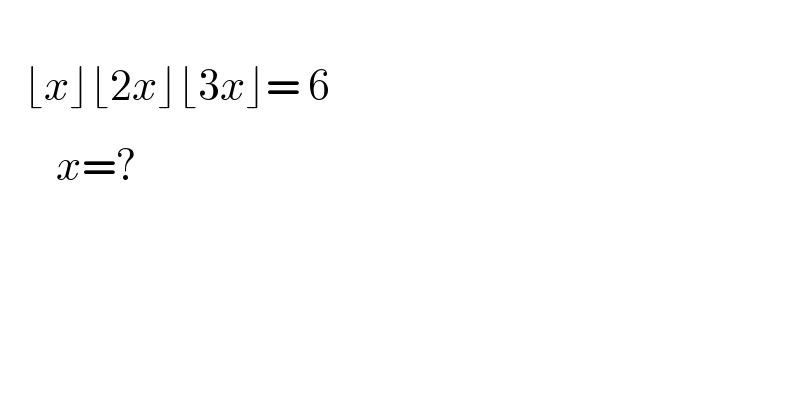
$$ \\ $$$$\:\:\:\lfloor{x}\rfloor\lfloor\mathrm{2}{x}\rfloor\lfloor\mathrm{3}{x}\rfloor=\:\mathrm{6} \\ $$$$\:\:\:\:\:\:\:{x}=\overset{} {?}\: \\ $$
Commented by MJS_new last updated on 16/Feb/22

$$\mathrm{1}\leqslant{x}<\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by mnjuly1970 last updated on 17/Feb/22

$$\:\:\checkmark\checkmark\:\:{thank}\:{you} \\ $$
Answered by mr W last updated on 17/Feb/22

$${say}\:{x}={n}+{f}\:{with}\:\mathrm{0}\leqslant{f}<\mathrm{1} \\ $$$$\mathrm{6}=\lfloor{x}\rfloor\lfloor\mathrm{2}{x}\rfloor\lfloor\mathrm{3}{x}\rfloor\geqslant{n}×\mathrm{2}{n}×\mathrm{3}{n}=\mathrm{6}{n}^{\mathrm{3}} \\ $$$$\Rightarrow{n}^{\mathrm{3}} \leqslant\mathrm{1}\:\Rightarrow{n}\leqslant\mathrm{1} \\ $$$$\mathrm{6}=\lfloor{x}\rfloor\lfloor\mathrm{2}{x}\rfloor\lfloor\mathrm{3}{x}\rfloor<{n}×\left(\mathrm{2}{n}+\mathrm{2}\right)×\left(\mathrm{3}{n}+\mathrm{3}\right)=\mathrm{6}{n}^{\mathrm{3}} +..+\mathrm{6} \\ $$$$\Rightarrow{n}>\mathrm{0} \\ $$$$\Rightarrow{n}=\mathrm{1} \\ $$$$\mathrm{1}×\left(\mathrm{2}+\lfloor\mathrm{2}{f}\rfloor\right)×\left(\mathrm{3}+\lfloor\mathrm{3}{f}\rfloor\right)=\mathrm{6} \\ $$$$\mathrm{6}+\mathrm{3}\lfloor\mathrm{2}{f}\rfloor+\mathrm{2}\lfloor\mathrm{3}{f}\rfloor+\lfloor\mathrm{2}{f}\rfloor\lfloor\mathrm{3}{f}\rfloor=\mathrm{6} \\ $$$$\mathrm{3}\lfloor\mathrm{2}{f}\rfloor+\mathrm{2}\lfloor\mathrm{3}{f}\rfloor+\lfloor\mathrm{2}{f}\rfloor\lfloor\mathrm{3}{f}\rfloor=\mathrm{0} \\ $$$$\Rightarrow\lfloor\mathrm{2}{f}\rfloor=\mathrm{0},\:\lfloor\mathrm{3}{f}\rfloor=\mathrm{0} \\ $$$$\Rightarrow\mathrm{0}\leqslant\mathrm{3}{f}<\mathrm{1}\:\Rightarrow\mathrm{0}\leqslant{f}<\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{solution}\:{is}\:\mathrm{1}+\mathrm{0}\leqslant{x}<\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}},\:{i}.{e}. \\ $$$$\mathrm{1}\leqslant{x}<\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by mnjuly1970 last updated on 17/Feb/22

$${thanks}\:{alot}\:{sir}\:{W} \\ $$
