
Question Number 16616 by Tinkutara last updated on 24/Jun/17
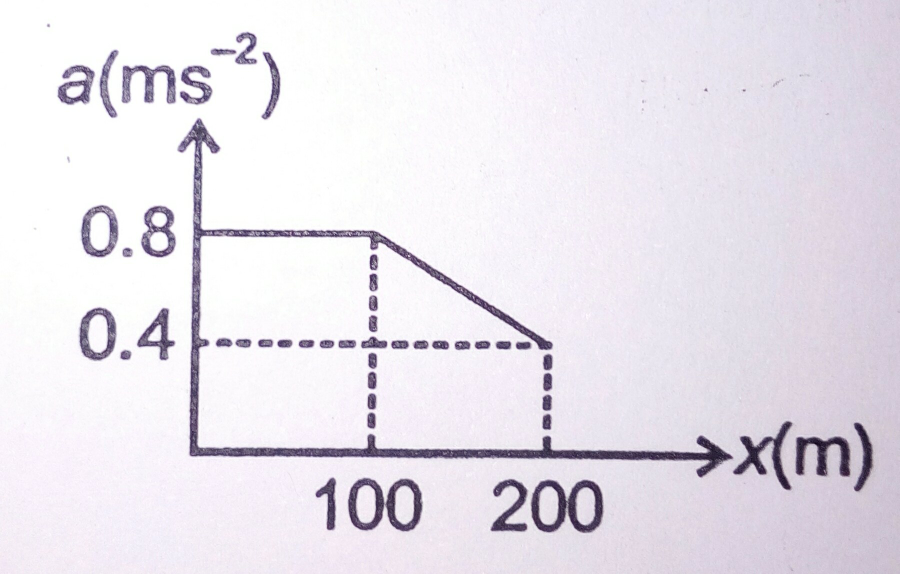
![A particle starts from the origin with velocity (√(44)) ms^(−1) on a straight horizontal road. Its acceleration varies with displacement as shown. The velocity of the particle as it passes through the position x = 0.2 km is [Answer: 18 ms^(−1) ]](Q16616.png)
$$\mathrm{A}\:\mathrm{particle}\:\mathrm{starts}\:\mathrm{from}\:\mathrm{the}\:\mathrm{origin}\:\mathrm{with} \\ $$$$\mathrm{velocity}\:\sqrt{\mathrm{44}}\:\mathrm{ms}^{−\mathrm{1}} \:\mathrm{on}\:\mathrm{a}\:\mathrm{straight} \\ $$$$\mathrm{horizontal}\:\mathrm{road}.\:\mathrm{Its}\:\mathrm{acceleration}\:\mathrm{varies} \\ $$$$\mathrm{with}\:\mathrm{displacement}\:\mathrm{as}\:\mathrm{shown}.\:\mathrm{The} \\ $$$$\mathrm{velocity}\:\mathrm{of}\:\mathrm{the}\:\mathrm{particle}\:\mathrm{as}\:\mathrm{it}\:\mathrm{passes} \\ $$$$\mathrm{through}\:\mathrm{the}\:\mathrm{position}\:{x}\:=\:\mathrm{0}.\mathrm{2}\:\mathrm{km}\:\mathrm{is} \\ $$$$\left[\mathrm{Answer}:\:\mathrm{18}\:\mathrm{ms}^{−\mathrm{1}} \right] \\ $$
Commented by Tinkutara last updated on 24/Jun/17
Answered by ajfour last updated on 24/Jun/17
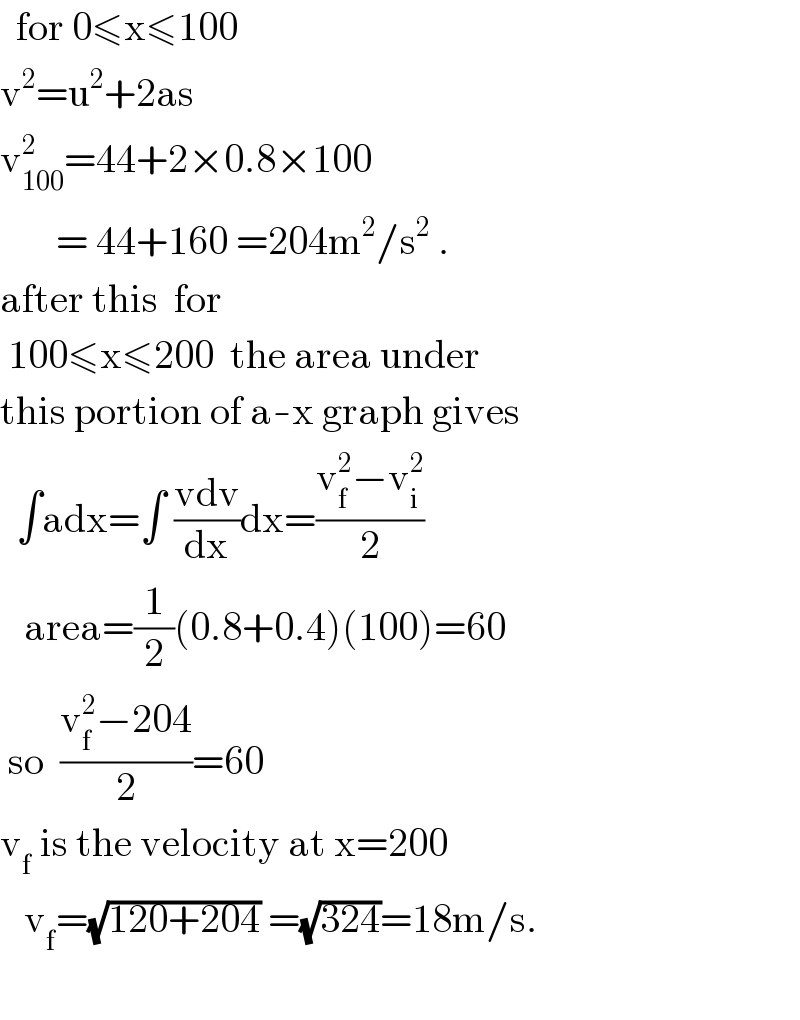
$$\:\:\mathrm{for}\:\mathrm{0}\leqslant\mathrm{x}\leqslant\mathrm{100} \\ $$$$\mathrm{v}^{\mathrm{2}} =\mathrm{u}^{\mathrm{2}} +\mathrm{2as} \\ $$$$\mathrm{v}_{\mathrm{100}} ^{\mathrm{2}} =\mathrm{44}+\mathrm{2}×\mathrm{0}.\mathrm{8}×\mathrm{100} \\ $$$$\:\:\:\:\:\:\:=\:\mathrm{44}+\mathrm{160}\:=\mathrm{204m}^{\mathrm{2}} /\mathrm{s}^{\mathrm{2}} \:. \\ $$$$\mathrm{after}\:\mathrm{this}\:\:\mathrm{for} \\ $$$$\:\mathrm{100}\leqslant\mathrm{x}\leqslant\mathrm{200}\:\:\mathrm{the}\:\mathrm{area}\:\mathrm{under} \\ $$$$\mathrm{this}\:\mathrm{portion}\:\mathrm{of}\:\mathrm{a}-\mathrm{x}\:\mathrm{graph}\:\mathrm{gives} \\ $$$$\:\:\int\mathrm{adx}=\int\:\frac{\mathrm{vdv}}{\mathrm{dx}}\mathrm{dx}=\frac{\mathrm{v}_{\mathrm{f}} ^{\mathrm{2}} −\mathrm{v}_{\mathrm{i}} ^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\:\:\:\mathrm{area}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{0}.\mathrm{8}+\mathrm{0}.\mathrm{4}\right)\left(\mathrm{100}\right)=\mathrm{60} \\ $$$$\:\mathrm{so}\:\:\frac{\mathrm{v}_{\mathrm{f}} ^{\mathrm{2}} −\mathrm{204}}{\mathrm{2}}=\mathrm{60}\:\:\:\:\:\: \\ $$$$\mathrm{v}_{\mathrm{f}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{velocity}\:\mathrm{at}\:\mathrm{x}=\mathrm{200}\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\mathrm{v}_{\mathrm{f}} =\sqrt{\mathrm{120}+\mathrm{204}}\:=\sqrt{\mathrm{324}}=\mathrm{18m}/\mathrm{s}. \\ $$$$ \\ $$
Commented by Tinkutara last updated on 24/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
