
Question Number 166036 by mr W last updated on 12/Feb/22
Commented by mr W last updated on 12/Feb/22
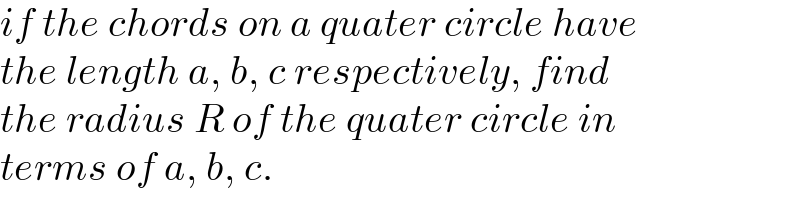
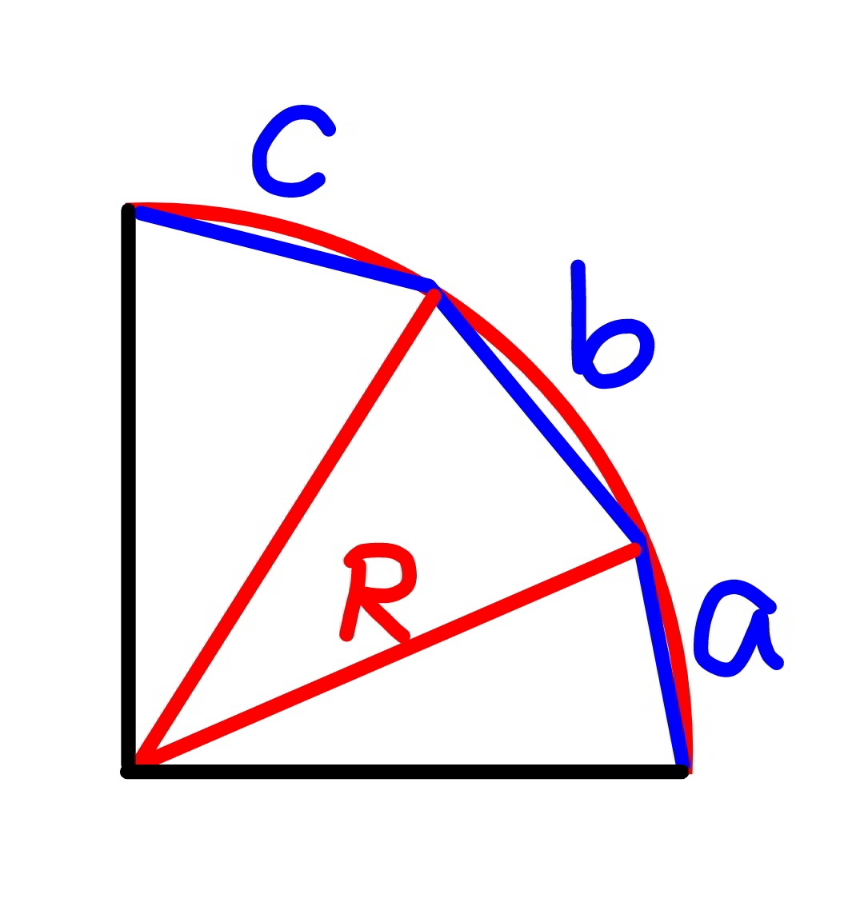
$${if}\:{the}\:{chords}\:{on}\:{a}\:{quater}\:{circle}\:{have} \\ $$$${the}\:{length}\:{a},\:{b},\:{c}\:{respectively},\:{find} \\ $$$${the}\:{radius}\:{R}\:{of}\:{the}\:{quater}\:{circle}\:{in} \\ $$$${terms}\:{of}\:{a},\:{b},\:{c}. \\ $$
Commented by ajfour last updated on 13/Feb/22

$${great}! \\ $$
Answered by Rasheed.Sindhi last updated on 12/Feb/22
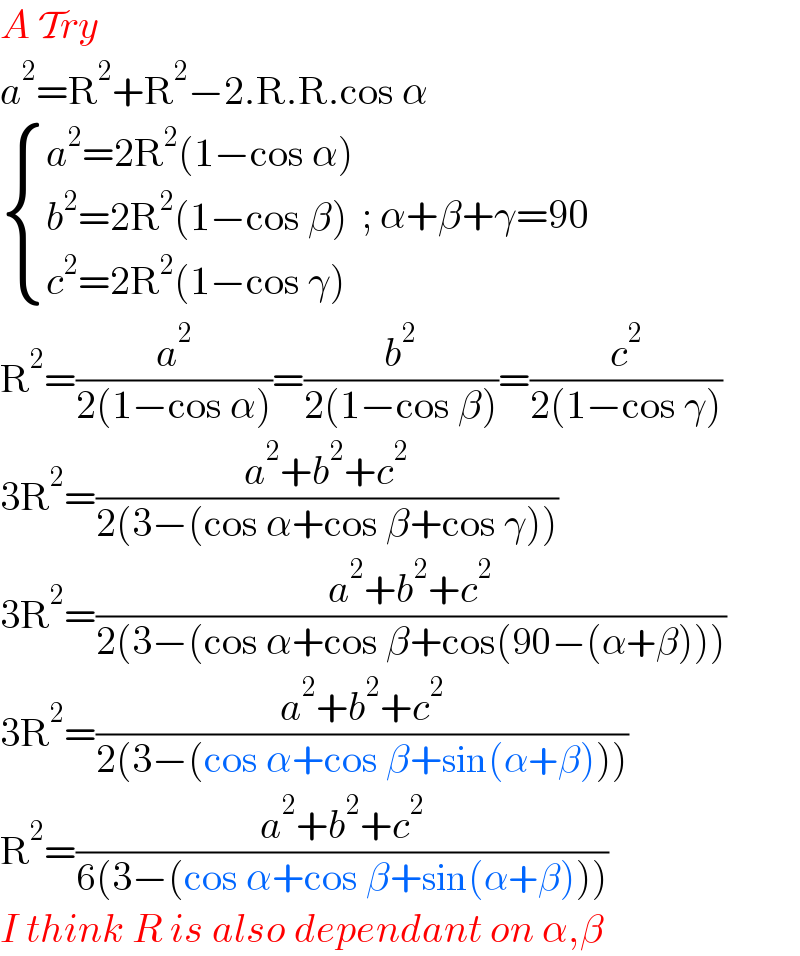
$${A}\:\mathcal{T}{ry} \\ $$$${a}^{\mathrm{2}} =\mathrm{R}^{\mathrm{2}} +\mathrm{R}^{\mathrm{2}} −\mathrm{2}.\mathrm{R}.\mathrm{R}.\mathrm{cos}\:\alpha \\ $$$$\begin{cases}{{a}^{\mathrm{2}} =\mathrm{2R}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\alpha\right)}\\{{b}^{\mathrm{2}} =\mathrm{2R}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\beta\right)}\\{{c}^{\mathrm{2}} =\mathrm{2R}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\gamma\right)}\end{cases}\:;\:\alpha+\beta+\gamma=\mathrm{90} \\ $$$$\mathrm{R}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\alpha\right)}=\frac{{b}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\beta\right)}=\frac{{c}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\gamma\right)} \\ $$$$\mathrm{3R}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{3}−\left(\mathrm{cos}\:\alpha+\mathrm{cos}\:\beta+\mathrm{cos}\:\gamma\right)\right)} \\ $$$$\mathrm{3R}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{3}−\left(\mathrm{cos}\:\alpha+\mathrm{cos}\:\beta+\mathrm{cos}\left(\mathrm{90}−\left(\alpha+\beta\right)\right)\right)\right.} \\ $$$$\mathrm{3R}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{3}−\left(\mathrm{cos}\:\alpha+\mathrm{cos}\:\beta+\mathrm{sin}\left(\alpha+\beta\right)\right)\right)} \\ $$$$\mathrm{R}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{6}\left(\mathrm{3}−\left(\mathrm{cos}\:\alpha+\mathrm{cos}\:\beta+\mathrm{sin}\left(\alpha+\beta\right)\right)\right)} \\ $$$${I}\:{think}\:{R}\:{is}\:{also}\:{dependant}\:{on}\:\alpha,\beta\: \\ $$
Commented by mr W last updated on 12/Feb/22

$${you}\:{have} \\ $$$$\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}=\frac{{a}}{\mathrm{2}{R}}\:\Rightarrow\frac{\alpha}{\mathrm{2}}=\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{\mathrm{2}{R}} \\ $$$$\mathrm{sin}\:\frac{\beta}{\mathrm{2}}=\frac{{b}}{\mathrm{2}{R}}\Rightarrow\frac{\beta}{\mathrm{2}}=\mathrm{sin}^{−\mathrm{1}} \frac{{b}}{\mathrm{2}{R}} \\ $$$$\mathrm{sin}\:\frac{\gamma}{\mathrm{2}}=\frac{{c}}{\mathrm{2}{R}}\Rightarrow\frac{\gamma}{\mathrm{2}}=\mathrm{sin}^{−\mathrm{1}} \frac{{c}}{\mathrm{2}{R}} \\ $$$$\frac{\alpha}{\mathrm{2}}+\frac{\beta}{\mathrm{2}}+\frac{\gamma}{\mathrm{2}}=\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{sin}^{−\mathrm{1}} \frac{{a}}{\mathrm{2}{R}}+\mathrm{sin}^{−\mathrm{1}} \frac{{b}}{\mathrm{2}{R}}+\mathrm{sin}^{−\mathrm{1}} \frac{{c}}{\mathrm{2}{R}}=\frac{\pi}{\mathrm{4}} \\ $$$${there}\:{is}\:{an}\:{unique}\:{solution}\:{for}\:{R}, \\ $$$${but}\:{we}\:{can}\:{not}\:{solve}\:{it}\:{in}\:{exact}\:{form} \\ $$$${in}\:{terms}\:{of}\:{a},\:{b},\:{c}. \\ $$
Commented by mahdipoor last updated on 12/Feb/22
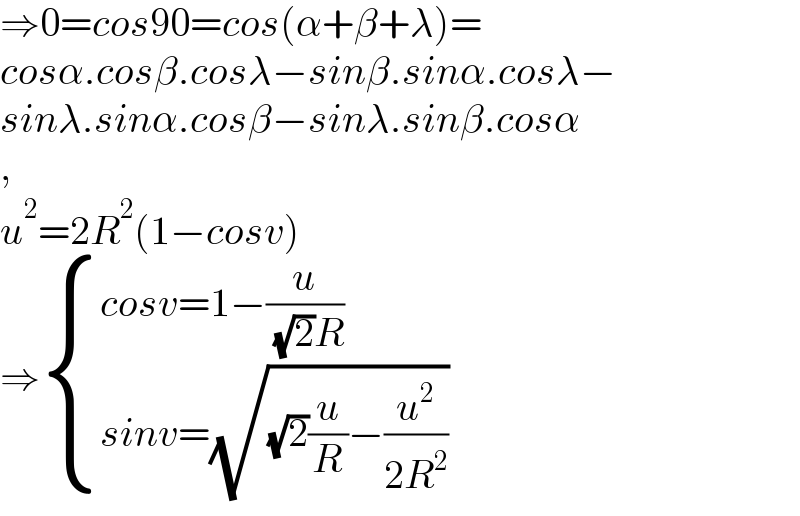
$$\Rightarrow\mathrm{0}={cos}\mathrm{90}={cos}\left(\alpha+\beta+\lambda\right)= \\ $$$${cos}\alpha.{cos}\beta.{cos}\lambda−{sin}\beta.{sin}\alpha.{cos}\lambda− \\ $$$${sin}\lambda.{sin}\alpha.{cos}\beta−{sin}\lambda.{sin}\beta.{cos}\alpha \\ $$$$, \\ $$$${u}^{\mathrm{2}} =\mathrm{2}{R}^{\mathrm{2}} \left(\mathrm{1}−{cosv}\right) \\ $$$$\Rightarrow\begin{cases}{{cosv}=\mathrm{1}−\frac{{u}}{\:\sqrt{\mathrm{2}}{R}}}\\{{sinv}=\sqrt{\sqrt{\mathrm{2}}\frac{{u}}{{R}}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}{R}^{\mathrm{2}} }}}\end{cases} \\ $$
Commented by Rasheed.Sindhi last updated on 12/Feb/22
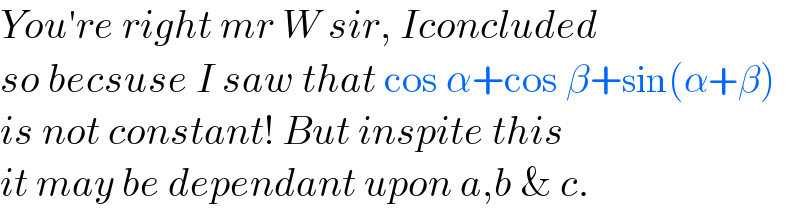
$${You}'{re}\:{right}\:{mr}\:{W}\:{sir},\:{Iconcluded} \\ $$$${so}\:{becsuse}\:{I}\:{saw}\:{that}\:\mathrm{cos}\:\alpha+\mathrm{cos}\:\beta+\mathrm{sin}\left(\alpha+\beta\right) \\ $$$${is}\:{not}\:{constant}!\:{But}\:{inspite}\:{this} \\ $$$${it}\:{may}\:{be}\:{dependant}\:{upon}\:{a},{b}\:\&\:{c}. \\ $$
Commented by mr W last updated on 13/Feb/22
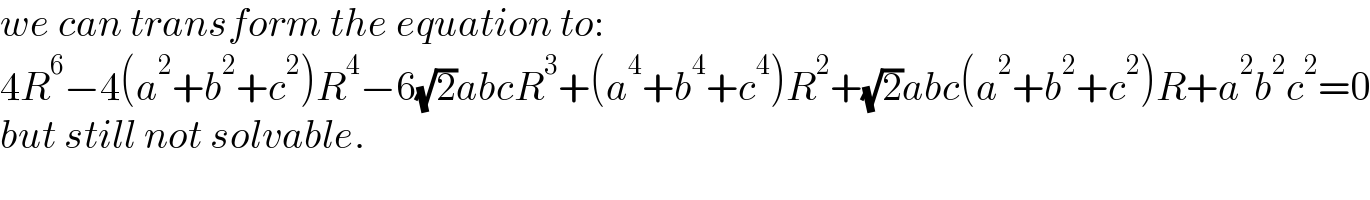
$${we}\:{can}\:{transform}\:{the}\:{equation}\:{to}: \\ $$$$\mathrm{4}{R}^{\mathrm{6}} −\mathrm{4}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right){R}^{\mathrm{4}} −\mathrm{6}\sqrt{\mathrm{2}}{abcR}^{\mathrm{3}} +\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \right){R}^{\mathrm{2}} +\sqrt{\mathrm{2}}{abc}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right){R}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} =\mathrm{0} \\ $$$${but}\:{still}\:{not}\:{solvable}. \\ $$
Commented by Rasheed.Sindhi last updated on 12/Feb/22
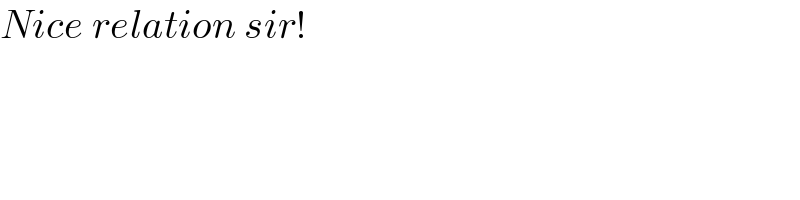
$${Nice}\:{relation}\:{sir}! \\ $$
Commented by ajfour last updated on 13/Feb/22
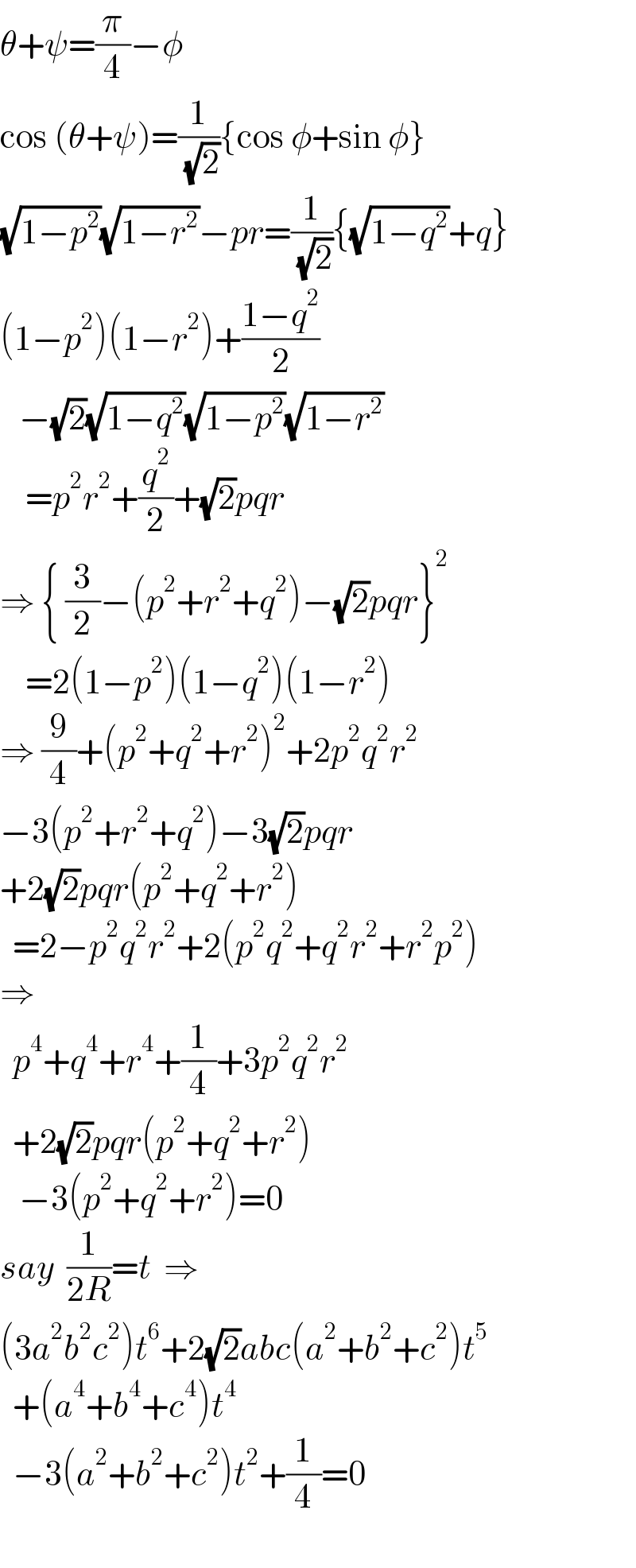
$$\theta+\psi=\frac{\pi}{\mathrm{4}}−\phi \\ $$$$\mathrm{cos}\:\left(\theta+\psi\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left\{\mathrm{cos}\:\phi+\mathrm{sin}\:\phi\right\} \\ $$$$\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }\sqrt{\mathrm{1}−{r}^{\mathrm{2}} }−{pr}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left\{\sqrt{\mathrm{1}−{q}^{\mathrm{2}} }+{q}\right\} \\ $$$$\left(\mathrm{1}−{p}^{\mathrm{2}} \right)\left(\mathrm{1}−{r}^{\mathrm{2}} \right)+\frac{\mathrm{1}−{q}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\:\:\:−\sqrt{\mathrm{2}}\sqrt{\mathrm{1}−{q}^{\mathrm{2}} }\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }\sqrt{\mathrm{1}−{r}^{\mathrm{2}} } \\ $$$$\:\:\:\:={p}^{\mathrm{2}} {r}^{\mathrm{2}} +\frac{{q}^{\mathrm{2}} }{\mathrm{2}}+\sqrt{\mathrm{2}}{pqr} \\ $$$$\Rightarrow\:\left\{\:\frac{\mathrm{3}}{\mathrm{2}}−\left({p}^{\mathrm{2}} +{r}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)−\sqrt{\mathrm{2}}{pqr}\right\}^{\mathrm{2}} \\ $$$$\:\:\:\:=\mathrm{2}\left(\mathrm{1}−{p}^{\mathrm{2}} \right)\left(\mathrm{1}−{q}^{\mathrm{2}} \right)\left(\mathrm{1}−{r}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\frac{\mathrm{9}}{\mathrm{4}}+\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{2}{p}^{\mathrm{2}} {q}^{\mathrm{2}} {r}^{\mathrm{2}} \\ $$$$−\mathrm{3}\left({p}^{\mathrm{2}} +{r}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)−\mathrm{3}\sqrt{\mathrm{2}}{pqr} \\ $$$$+\mathrm{2}\sqrt{\mathrm{2}}{pqr}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right) \\ $$$$\:\:=\mathrm{2}−{p}^{\mathrm{2}} {q}^{\mathrm{2}} {r}^{\mathrm{2}} +\mathrm{2}\left({p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} \right) \\ $$$$\Rightarrow \\ $$$$\:\:{p}^{\mathrm{4}} +{q}^{\mathrm{4}} +{r}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{3}{p}^{\mathrm{2}} {q}^{\mathrm{2}} {r}^{\mathrm{2}} \\ $$$$\:\:+\mathrm{2}\sqrt{\mathrm{2}}{pqr}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right) \\ $$$$\:\:\:−\mathrm{3}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${say}\:\:\frac{\mathrm{1}}{\mathrm{2}{R}}={t}\:\:\Rightarrow \\ $$$$\left(\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} \right){t}^{\mathrm{6}} +\mathrm{2}\sqrt{\mathrm{2}}{abc}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right){t}^{\mathrm{5}} \\ $$$$\:\:+\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \right){t}^{\mathrm{4}} \\ $$$$\:\:−\mathrm{3}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right){t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$ \\ $$
Answered by ajfour last updated on 15/Feb/22
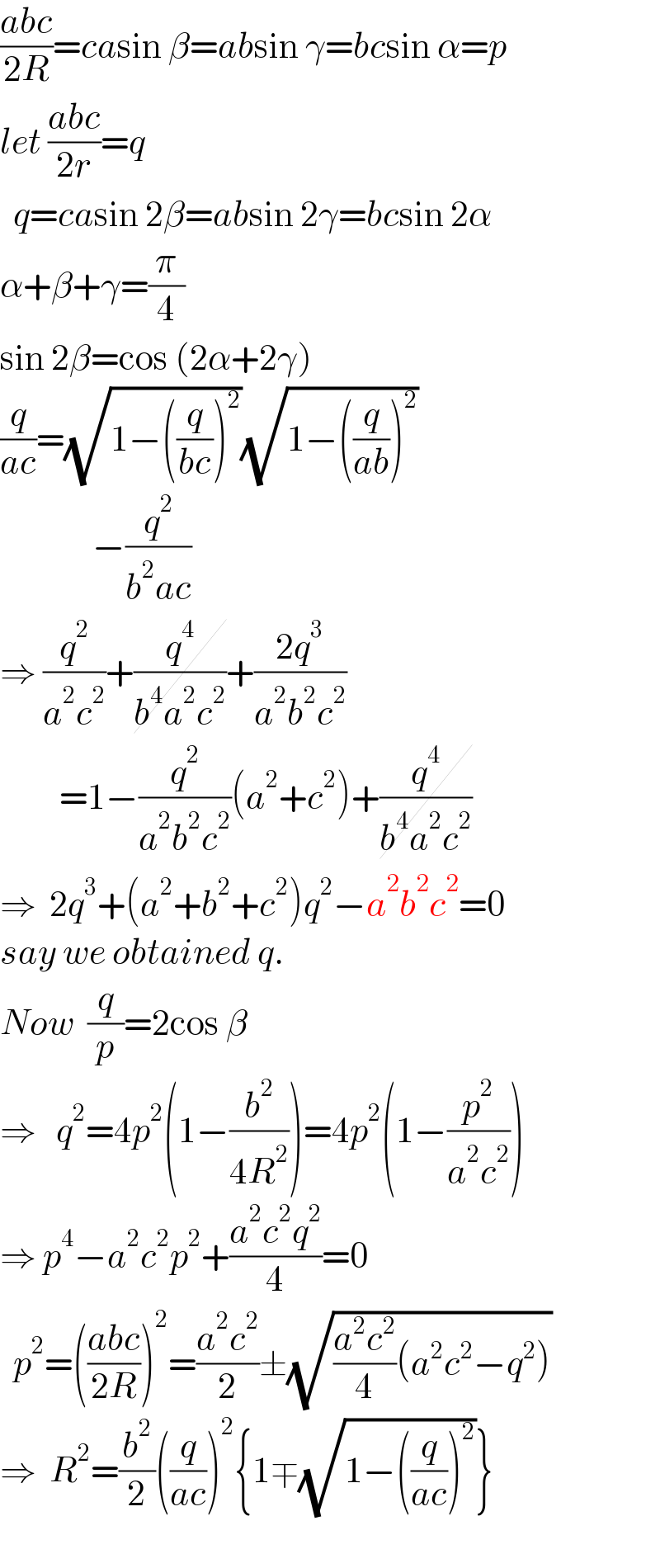
$$\frac{{abc}}{\mathrm{2}{R}}={ca}\mathrm{sin}\:\beta={ab}\mathrm{sin}\:\gamma={bc}\mathrm{sin}\:\alpha={p} \\ $$$${let}\:\frac{{abc}}{\mathrm{2}{r}}={q} \\ $$$$\:\:{q}={ca}\mathrm{sin}\:\mathrm{2}\beta={ab}\mathrm{sin}\:\mathrm{2}\gamma={bc}\mathrm{sin}\:\mathrm{2}\alpha \\ $$$$\alpha+\beta+\gamma=\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{sin}\:\mathrm{2}\beta=\mathrm{cos}\:\left(\mathrm{2}\alpha+\mathrm{2}\gamma\right) \\ $$$$\frac{{q}}{{ac}}=\sqrt{\mathrm{1}−\left(\frac{{q}}{{bc}}\right)^{\mathrm{2}} }\sqrt{\mathrm{1}−\left(\frac{{q}}{{ab}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{{q}^{\mathrm{2}} }{{b}^{\mathrm{2}} {ac}} \\ $$$$\Rightarrow\:\frac{{q}^{\mathrm{2}} }{{a}^{\mathrm{2}} {c}^{\mathrm{2}} }+\cancel{\frac{{q}^{\mathrm{4}} }{{b}^{\mathrm{4}} {a}^{\mathrm{2}} {c}^{\mathrm{2}} }}+\frac{\mathrm{2}{q}^{\mathrm{3}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{1}−\frac{{q}^{\mathrm{2}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} }\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)+\cancel{\frac{{q}^{\mathrm{4}} }{{b}^{\mathrm{4}} {a}^{\mathrm{2}} {c}^{\mathrm{2}} }} \\ $$$$\Rightarrow\:\:\mathrm{2}{q}^{\mathrm{3}} +\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right){q}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} =\mathrm{0} \\ $$$${say}\:{we}\:{obtained}\:{q}.\:\:\: \\ $$$${Now}\:\:\frac{{q}}{{p}}=\mathrm{2cos}\:\beta \\ $$$$\Rightarrow\:\:\:{q}^{\mathrm{2}} =\mathrm{4}{p}^{\mathrm{2}} \left(\mathrm{1}−\frac{{b}^{\mathrm{2}} }{\mathrm{4}{R}^{\mathrm{2}} }\right)=\mathrm{4}{p}^{\mathrm{2}} \left(\mathrm{1}−\frac{{p}^{\mathrm{2}} }{{a}^{\mathrm{2}} {c}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\:{p}^{\mathrm{4}} −{a}^{\mathrm{2}} {c}^{\mathrm{2}} {p}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} {c}^{\mathrm{2}} {q}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0} \\ $$$$\:\:{p}^{\mathrm{2}} =\left(\frac{{abc}}{\mathrm{2}{R}}\right)^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} {c}^{\mathrm{2}} }{\mathrm{2}}\pm\sqrt{\frac{{a}^{\mathrm{2}} {c}^{\mathrm{2}} }{\mathrm{4}}\left({a}^{\mathrm{2}} {c}^{\mathrm{2}} −{q}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow\:\:{R}^{\mathrm{2}} =\frac{{b}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{{q}}{{ac}}\right)^{\mathrm{2}} \left\{\mathrm{1}\mp\sqrt{\mathrm{1}−\left(\frac{{q}}{{ac}}\right)^{\mathrm{2}} }\right\} \\ $$$$ \\ $$
Commented by ajfour last updated on 15/Feb/22
Commented by mr W last updated on 15/Feb/22
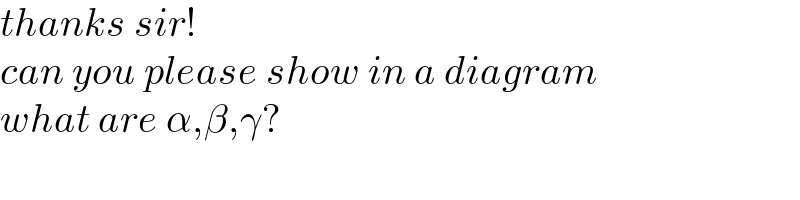
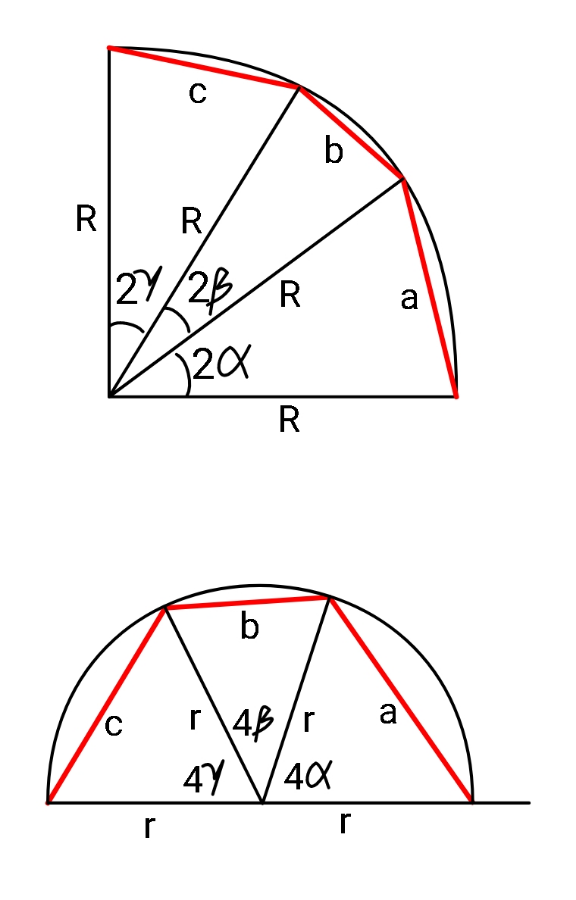
$${thanks}\:{sir}! \\ $$$${can}\:{you}\:{please}\:{show}\:{in}\:{a}\:{diagram} \\ $$$${what}\:{are}\:\alpha,\beta,\gamma? \\ $$
Commented by mr W last updated on 15/Feb/22
Commented by mr W last updated on 15/Feb/22
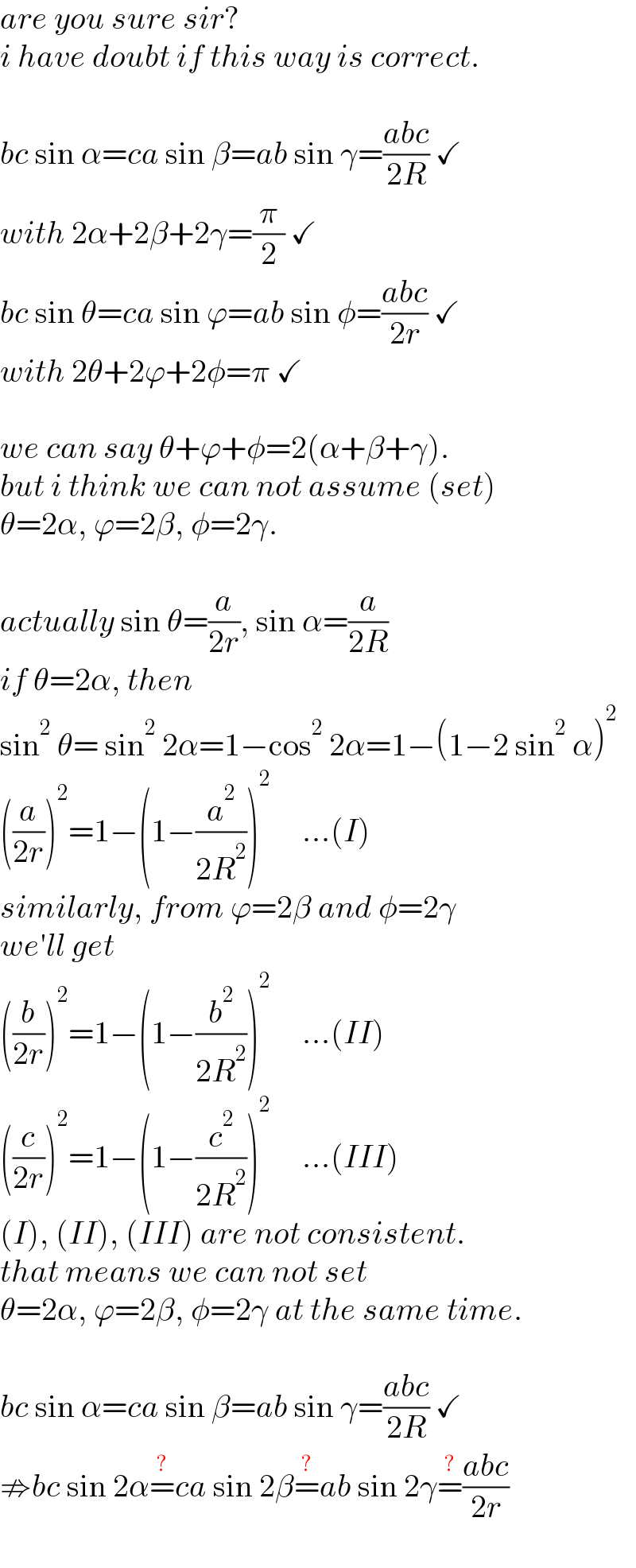
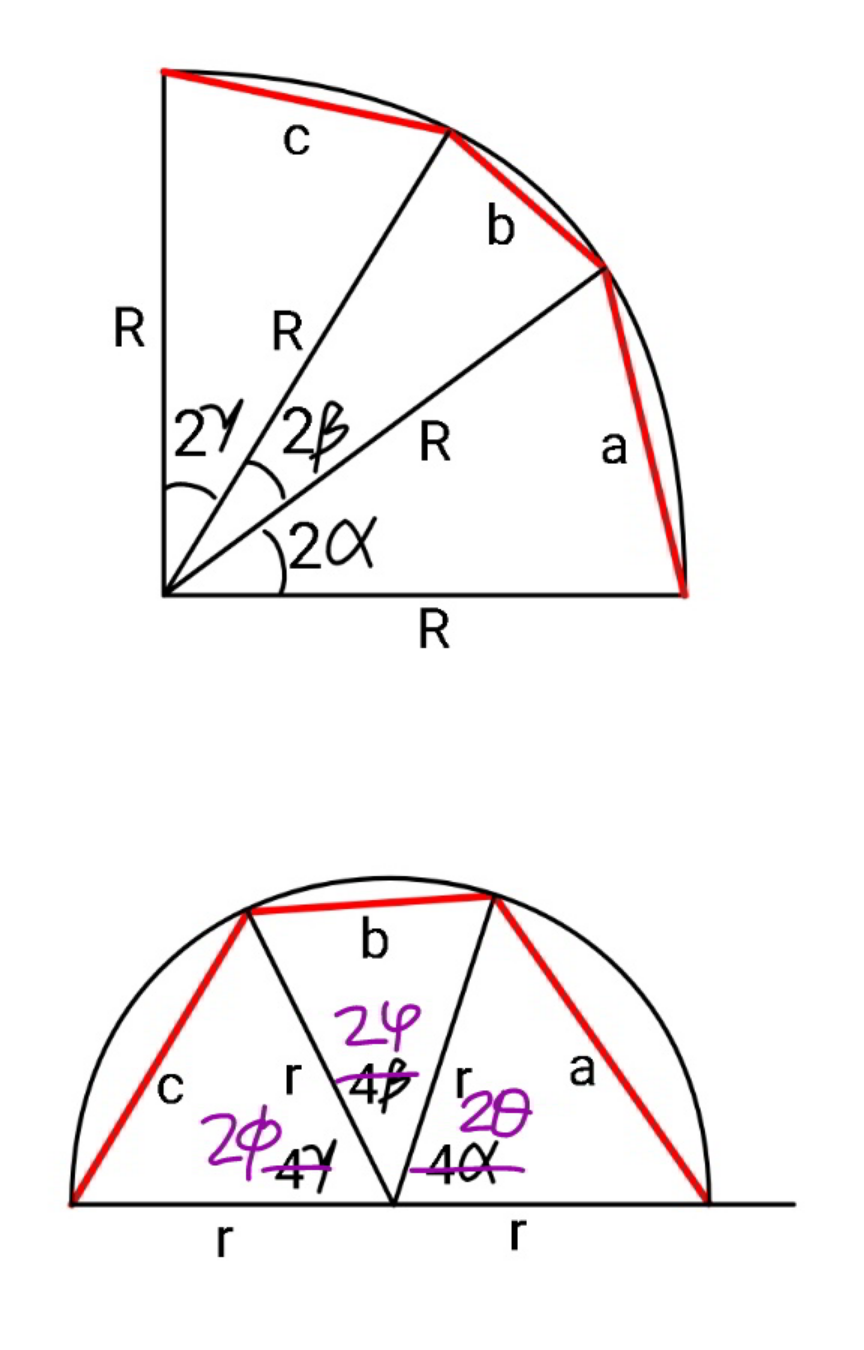
$${are}\:{you}\:{sure}\:{sir}? \\ $$$${i}\:{have}\:{doubt}\:{if}\:{this}\:{way}\:{is}\:{correct}. \\ $$$$ \\ $$$${bc}\:\mathrm{sin}\:\alpha={ca}\:\mathrm{sin}\:\beta={ab}\:\mathrm{sin}\:\gamma=\frac{{abc}}{\mathrm{2}{R}}\:\checkmark \\ $$$${with}\:\mathrm{2}\alpha+\mathrm{2}\beta+\mathrm{2}\gamma=\frac{\pi}{\mathrm{2}}\:\checkmark \\ $$$${bc}\:\mathrm{sin}\:\theta={ca}\:\mathrm{sin}\:\varphi={ab}\:\mathrm{sin}\:\phi=\frac{{abc}}{\mathrm{2}{r}}\:\checkmark \\ $$$${with}\:\mathrm{2}\theta+\mathrm{2}\varphi+\mathrm{2}\phi=\pi\:\checkmark \\ $$$$ \\ $$$${we}\:{can}\:{say}\:\theta+\varphi+\phi=\mathrm{2}\left(\alpha+\beta+\gamma\right). \\ $$$${but}\:{i}\:{think}\:{we}\:{can}\:{not}\:{assume}\:\left({set}\right) \\ $$$$\theta=\mathrm{2}\alpha,\:\varphi=\mathrm{2}\beta,\:\phi=\mathrm{2}\gamma. \\ $$$$ \\ $$$${actually}\:\mathrm{sin}\:\theta=\frac{{a}}{\mathrm{2}{r}},\:\mathrm{sin}\:\alpha=\frac{{a}}{\mathrm{2}{R}} \\ $$$${if}\:\theta=\mathrm{2}\alpha,\:{then} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\theta=\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}\alpha=\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}\alpha=\mathrm{1}−\left(\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\alpha\right)^{\mathrm{2}} \\ $$$$\left(\frac{{a}}{\mathrm{2}{r}}\right)^{\mathrm{2}} =\mathrm{1}−\left(\mathrm{1}−\frac{{a}^{\mathrm{2}} }{\mathrm{2}{R}^{\mathrm{2}} }\right)^{\mathrm{2}} \:\:\:\:\:...\left({I}\right) \\ $$$${similarly},\:{from}\:\varphi=\mathrm{2}\beta\:{and}\:\phi=\mathrm{2}\gamma \\ $$$${we}'{ll}\:{get} \\ $$$$\left(\frac{{b}}{\mathrm{2}{r}}\right)^{\mathrm{2}} =\mathrm{1}−\left(\mathrm{1}−\frac{{b}^{\mathrm{2}} }{\mathrm{2}{R}^{\mathrm{2}} }\right)^{\mathrm{2}} \:\:\:\:\:...\left({II}\right) \\ $$$$\left(\frac{{c}}{\mathrm{2}{r}}\right)^{\mathrm{2}} =\mathrm{1}−\left(\mathrm{1}−\frac{{c}^{\mathrm{2}} }{\mathrm{2}{R}^{\mathrm{2}} }\right)^{\mathrm{2}} \:\:\:\:\:...\left({III}\right) \\ $$$$\left({I}\right),\:\left({II}\right),\:\left({III}\right)\:{are}\:{not}\:{consistent}. \\ $$$${that}\:{means}\:{we}\:{can}\:{not}\:{set} \\ $$$$\theta=\mathrm{2}\alpha,\:\varphi=\mathrm{2}\beta,\:\phi=\mathrm{2}\gamma\:{at}\:{the}\:{same}\:{time}. \\ $$$$ \\ $$$${bc}\:\mathrm{sin}\:\alpha={ca}\:\mathrm{sin}\:\beta={ab}\:\mathrm{sin}\:\gamma=\frac{{abc}}{\mathrm{2}{R}}\:\checkmark \\ $$$$\nRightarrow{bc}\:\mathrm{sin}\:\mathrm{2}\alpha\overset{?} {=}{ca}\:\mathrm{sin}\:\mathrm{2}\beta\overset{?} {=}{ab}\:\mathrm{sin}\:\mathrm{2}\gamma\overset{?} {=}\frac{{abc}}{\mathrm{2}{r}}\: \\ $$
