
Question Number 165950 by mathlove last updated on 10/Feb/22
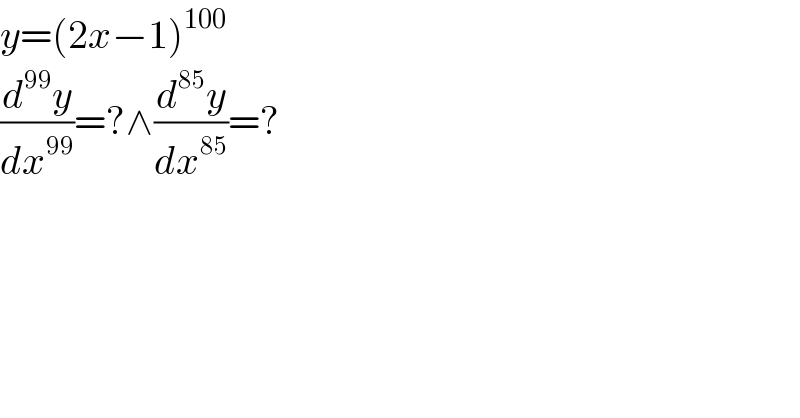
$${y}=\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{100}} \\ $$$$\frac{{d}^{\mathrm{99}} {y}}{{dx}^{\mathrm{99}} }=?\wedge\frac{{d}^{\mathrm{85}} {y}}{{dx}^{\mathrm{85}} }=? \\ $$
Answered by qaz last updated on 10/Feb/22

$$\mathrm{y}^{\left(\mathrm{1}\right)} =\mathrm{2}\left(\mathrm{2x}−\mathrm{1}\right)^{\mathrm{99}} \\ $$$$\mathrm{y}^{\left(\mathrm{2}\right)} =\mathrm{2}^{\mathrm{2}} \left(\mathrm{2x}−\mathrm{1}\right)^{\mathrm{98}} \\ $$$$... \\ $$$$\mathrm{y}^{\left(\mathrm{99}\right)} =\mathrm{2}^{\mathrm{99}} \left(\mathrm{2x}−\mathrm{1}\right) \\ $$$$\mathrm{y}^{\left(\mathrm{85}\right)} =\mathrm{2}^{\mathrm{85}} \left(\mathrm{2x}−\mathrm{1}\right)^{\mathrm{15}} \\ $$
Commented by MJS_new last updated on 10/Feb/22
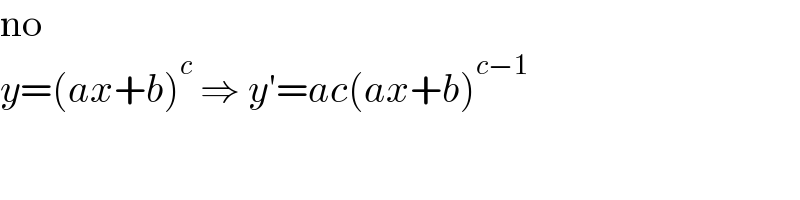
$$\mathrm{no} \\ $$$${y}=\left({ax}+{b}\right)^{{c}} \:\Rightarrow\:{y}'={ac}\left({ax}+{b}\right)^{{c}−\mathrm{1}} \\ $$
