
Question Number 165900 by cherokeesay last updated on 09/Feb/22
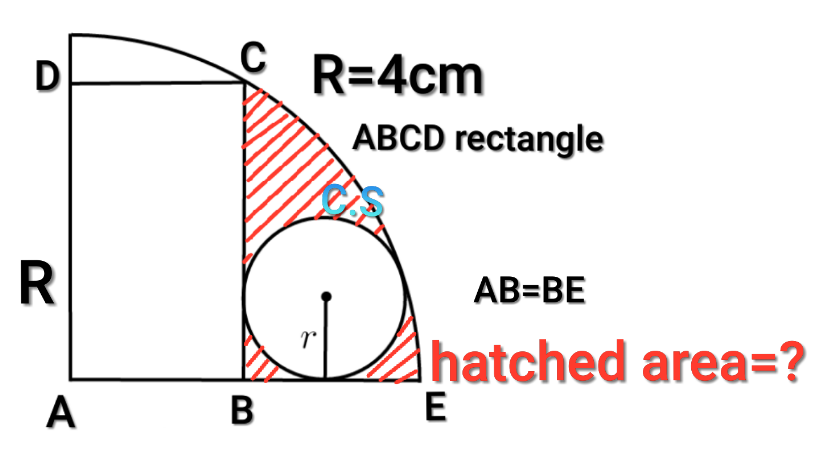
Commented by som(math1967) last updated on 10/Feb/22
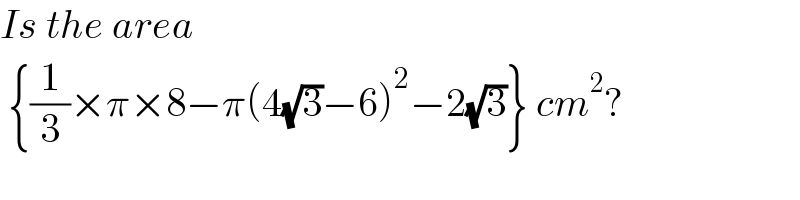
$${Is}\:{the}\:{area} \\ $$$$\:\left\{\frac{\mathrm{1}}{\mathrm{3}}×\pi×\mathrm{8}−\pi\left(\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{6}\right)^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}\right\}\:{cm}^{\mathrm{2}} ? \\ $$
Commented by cherokeesay last updated on 10/Feb/22

$$\backsimeq\:\mathrm{2},\mathrm{2} \\ $$$${goog}\:{answer}\:! \\ $$$${thank}\:{you}. \\ $$
Commented by som(math1967) last updated on 10/Feb/22
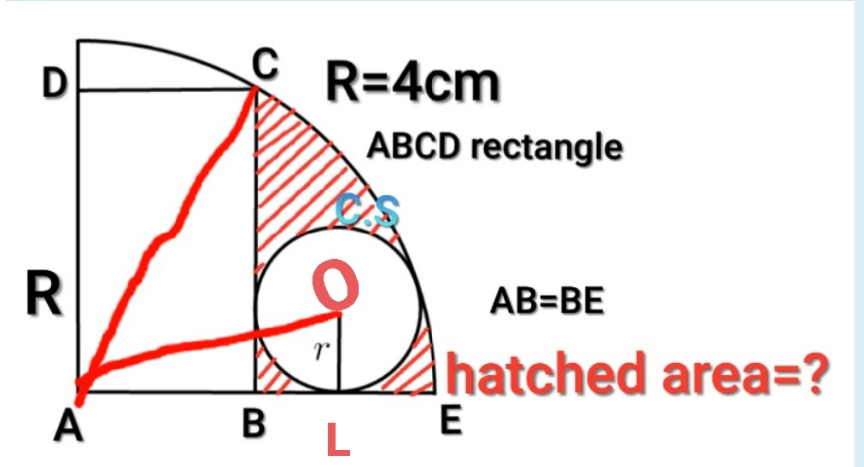
Commented by som(math1967) last updated on 10/Feb/22
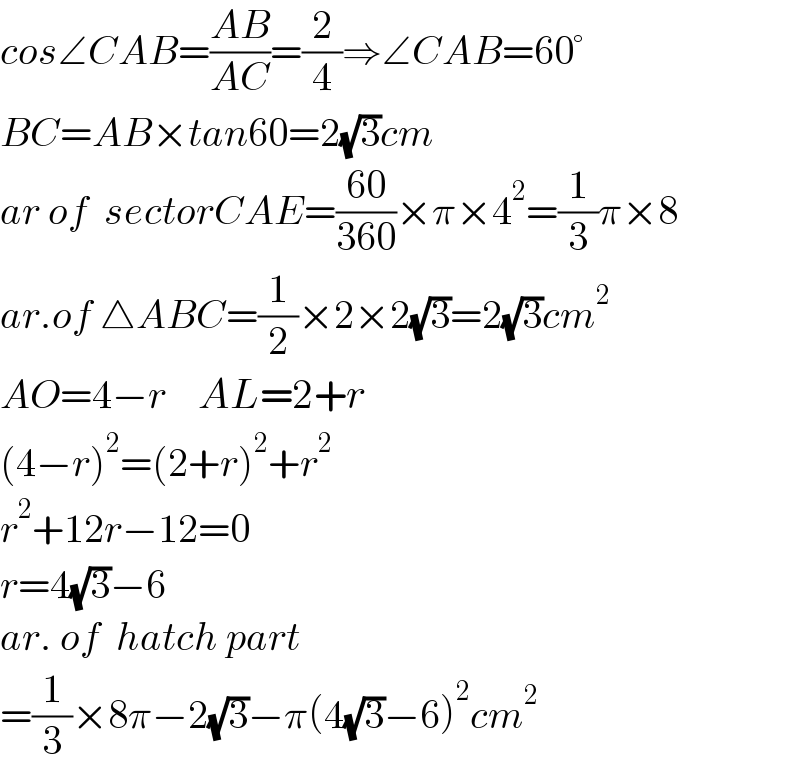
$${cos}\angle{CAB}=\frac{{AB}}{{AC}}=\frac{\mathrm{2}}{\mathrm{4}}\Rightarrow\angle{CAB}=\mathrm{60}° \\ $$$${BC}={AB}×{tan}\mathrm{60}=\mathrm{2}\sqrt{\mathrm{3}}{cm} \\ $$$${ar}\:{of}\:\:{sectorCAE}=\frac{\mathrm{60}}{\mathrm{360}}×\pi×\mathrm{4}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}}\pi×\mathrm{8} \\ $$$${ar}.{of}\:\bigtriangleup{ABC}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}×\mathrm{2}\sqrt{\mathrm{3}}=\mathrm{2}\sqrt{\mathrm{3}}{cm}^{\mathrm{2}} \\ $$$${AO}=\mathrm{4}−{r}\:\:\:\:{AL}=\mathrm{2}+{r} \\ $$$$\left(\mathrm{4}−{r}\right)^{\mathrm{2}} =\left(\mathrm{2}+{r}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} +\mathrm{12}{r}−\mathrm{12}=\mathrm{0} \\ $$$${r}=\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{6} \\ $$$${ar}.\:{of}\:\:{hatch}\:{part} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}×\mathrm{8}\pi−\mathrm{2}\sqrt{\mathrm{3}}−\pi\left(\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{6}\right)^{\mathrm{2}} {cm}^{\mathrm{2}} \\ $$
Commented by Tawa11 last updated on 10/Feb/22

$$\mathrm{Weldone}\:\mathrm{sir} \\ $$
Answered by Eulerian last updated on 10/Feb/22
![Solution: Given that: a = 2 cm b = (√(4^2 −2^2 )) = 2(√3) cm sin(θ) = (1/2) ⇒ θ = 30° (4−r)^2 = r^2 +(2+r)^2 r^2 +12r−12 = 0 By quadratic formula: r = ((−12+(√(12^2 +4(12))))/2) = 4(√3)−6 cm ∴ Area_(hatched) = ((π(4^2 ))/4) − [π(4(√3)−6)^2 + ((2(4))/2) + (((30°)/(360°)))∙π(4)^2 ] = (48π(√3) − ((244π)/3) − 4) cm^2](Q165948.png)
$$ \\ $$$$\:\boldsymbol{\mathrm{Solution}}: \\ $$$$\:\mathrm{Given}\:\mathrm{that}: \\ $$$$\:\mathrm{a}\:=\:\mathrm{2}\:\mathrm{cm} \\ $$$$\:\mathrm{b}\:=\:\sqrt{\mathrm{4}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }\:=\:\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{cm} \\ $$$$\:\mathrm{sin}\left(\theta\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\:\Rightarrow\:\:\theta\:=\:\mathrm{30}° \\ $$$$\:\left(\mathrm{4}−\mathrm{r}\right)^{\mathrm{2}} \:=\:\mathrm{r}^{\mathrm{2}} +\left(\mathrm{2}+\mathrm{r}\right)^{\mathrm{2}} \\ $$$$\:\mathrm{r}^{\mathrm{2}} +\mathrm{12r}−\mathrm{12}\:=\:\mathrm{0} \\ $$$$\:\mathrm{By}\:\mathrm{quadratic}\:\mathrm{formula}: \\ $$$$\:\mathrm{r}\:=\:\frac{−\mathrm{12}+\sqrt{\mathrm{12}^{\mathrm{2}} +\mathrm{4}\left(\mathrm{12}\right)}}{\mathrm{2}}\:=\:\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{6}\:\:\mathrm{cm} \\ $$$$\: \\ $$$$\:\therefore \\ $$$$\:\mathrm{Area}_{\mathrm{hatched}} \:=\:\frac{\pi\left(\mathrm{4}^{\mathrm{2}} \right)}{\mathrm{4}}\:−\:\left[\pi\left(\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{6}\right)^{\mathrm{2}} \:+\:\frac{\mathrm{2}\left(\mathrm{4}\right)}{\mathrm{2}}\:+\:\left(\frac{\mathrm{30}°}{\mathrm{360}°}\right)\centerdot\pi\left(\mathrm{4}\right)^{\mathrm{2}} \right]\:=\:\left(\mathrm{48}\pi\sqrt{\mathrm{3}}\:−\:\frac{\mathrm{244}\pi}{\mathrm{3}}\:−\:\mathrm{4}\right)\:\mathrm{cm}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\: \\ $$
Commented by cherokeesay last updated on 10/Feb/22

$${please},\:{try}\:{again}\:! \\ $$
