
Question Number 165881 by bounhome last updated on 09/Feb/22
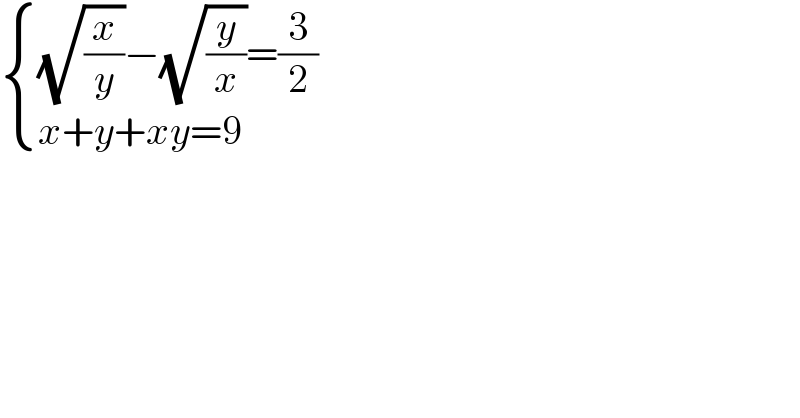
$$\begin{cases}{\sqrt{\frac{{x}}{{y}}}−\sqrt{\frac{{y}}{{x}}}=\frac{\mathrm{3}}{\mathrm{2}}}\\{{x}+{y}+{xy}=\mathrm{9}}\end{cases} \\ $$
Answered by Rasheed.Sindhi last updated on 09/Feb/22
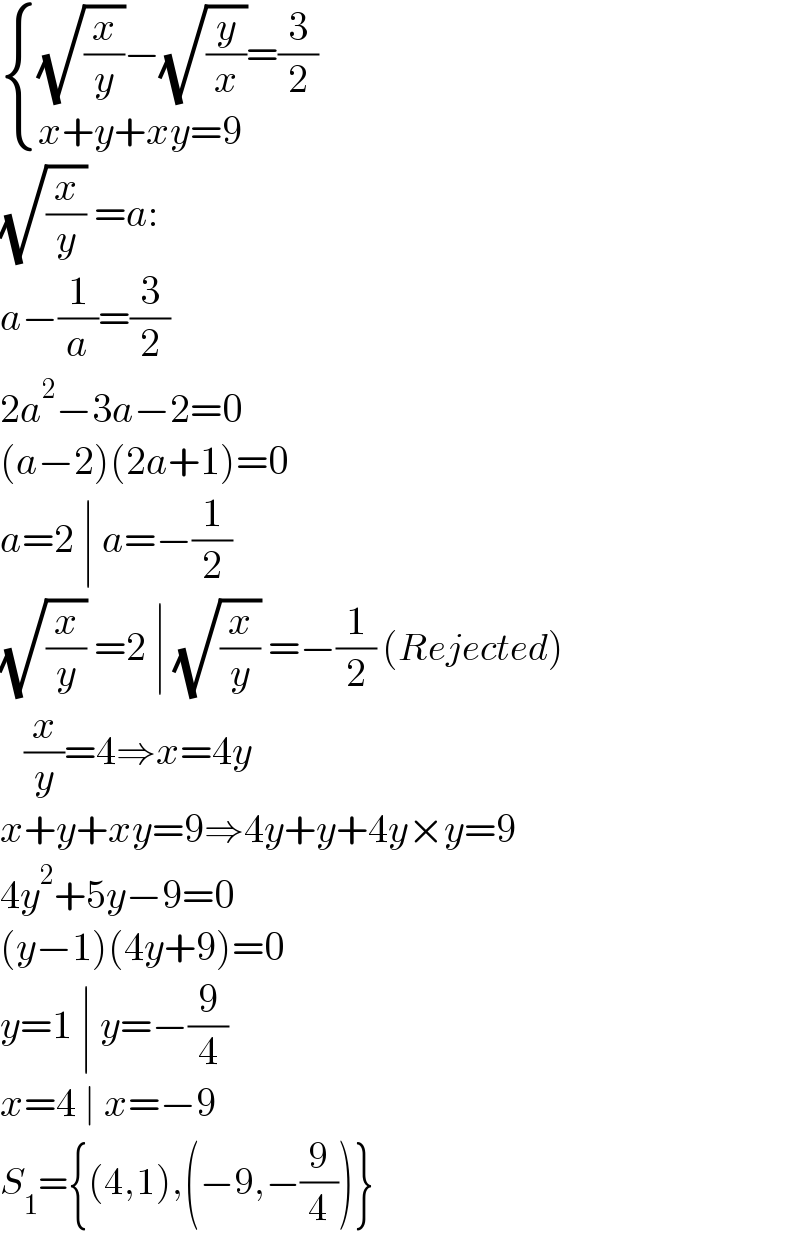
$$\begin{cases}{\sqrt{\frac{{x}}{{y}}}−\sqrt{\frac{{y}}{{x}}}=\frac{\mathrm{3}}{\mathrm{2}}}\\{{x}+{y}+{xy}=\mathrm{9}}\end{cases} \\ $$$$\sqrt{\frac{{x}}{{y}}}\:={a}: \\ $$$${a}−\frac{\mathrm{1}}{{a}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{2}{a}^{\mathrm{2}} −\mathrm{3}{a}−\mathrm{2}=\mathrm{0} \\ $$$$\left({a}−\mathrm{2}\right)\left(\mathrm{2}{a}+\mathrm{1}\right)=\mathrm{0} \\ $$$${a}=\mathrm{2}\:\mid\:{a}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\sqrt{\frac{{x}}{{y}}}\:=\mathrm{2}\:\mid\:\sqrt{\frac{{x}}{{y}}}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\left({Rejected}\right) \\ $$$$\:\:\:\frac{{x}}{{y}}=\mathrm{4}\Rightarrow{x}=\mathrm{4}{y} \\ $$$${x}+{y}+{xy}=\mathrm{9}\Rightarrow\mathrm{4}{y}+{y}+\mathrm{4}{y}×{y}=\mathrm{9} \\ $$$$\mathrm{4}{y}^{\mathrm{2}} +\mathrm{5}{y}−\mathrm{9}=\mathrm{0} \\ $$$$\left({y}−\mathrm{1}\right)\left(\mathrm{4}{y}+\mathrm{9}\right)=\mathrm{0} \\ $$$${y}=\mathrm{1}\:\mid\:{y}=−\frac{\mathrm{9}}{\mathrm{4}} \\ $$$${x}=\mathrm{4}\:\mid\:{x}=−\mathrm{9} \\ $$$${S}_{\mathrm{1}} =\left\{\left(\mathrm{4},\mathrm{1}\right),\left(−\mathrm{9},−\frac{\mathrm{9}}{\mathrm{4}}\right)\right\} \\ $$
Answered by MJS_new last updated on 09/Feb/22
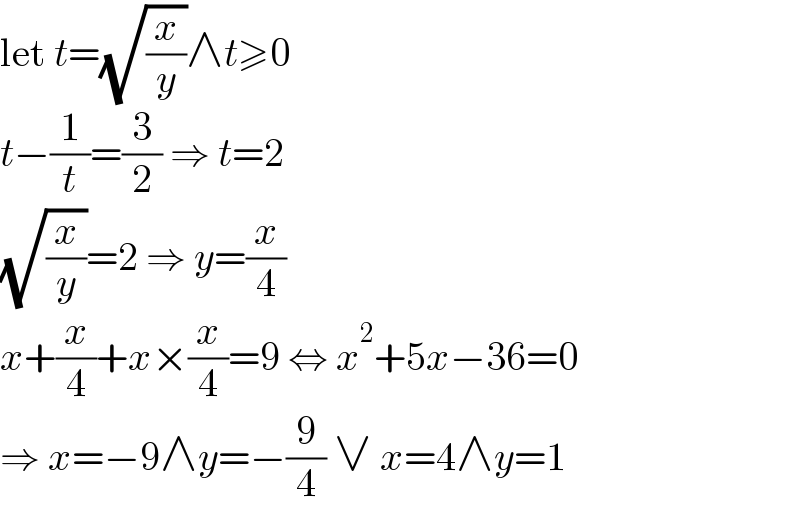
$$\mathrm{let}\:{t}=\sqrt{\frac{{x}}{{y}}}\wedge{t}\geqslant\mathrm{0} \\ $$$${t}−\frac{\mathrm{1}}{{t}}=\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow\:{t}=\mathrm{2} \\ $$$$\sqrt{\frac{{x}}{{y}}}=\mathrm{2}\:\Rightarrow\:{y}=\frac{{x}}{\mathrm{4}} \\ $$$${x}+\frac{{x}}{\mathrm{4}}+{x}×\frac{{x}}{\mathrm{4}}=\mathrm{9}\:\Leftrightarrow\:{x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{36}=\mathrm{0} \\ $$$$\Rightarrow\:{x}=−\mathrm{9}\wedge{y}=−\frac{\mathrm{9}}{\mathrm{4}}\:\vee\:{x}=\mathrm{4}\wedge{y}=\mathrm{1} \\ $$
Answered by Rasheed.Sindhi last updated on 10/Feb/22
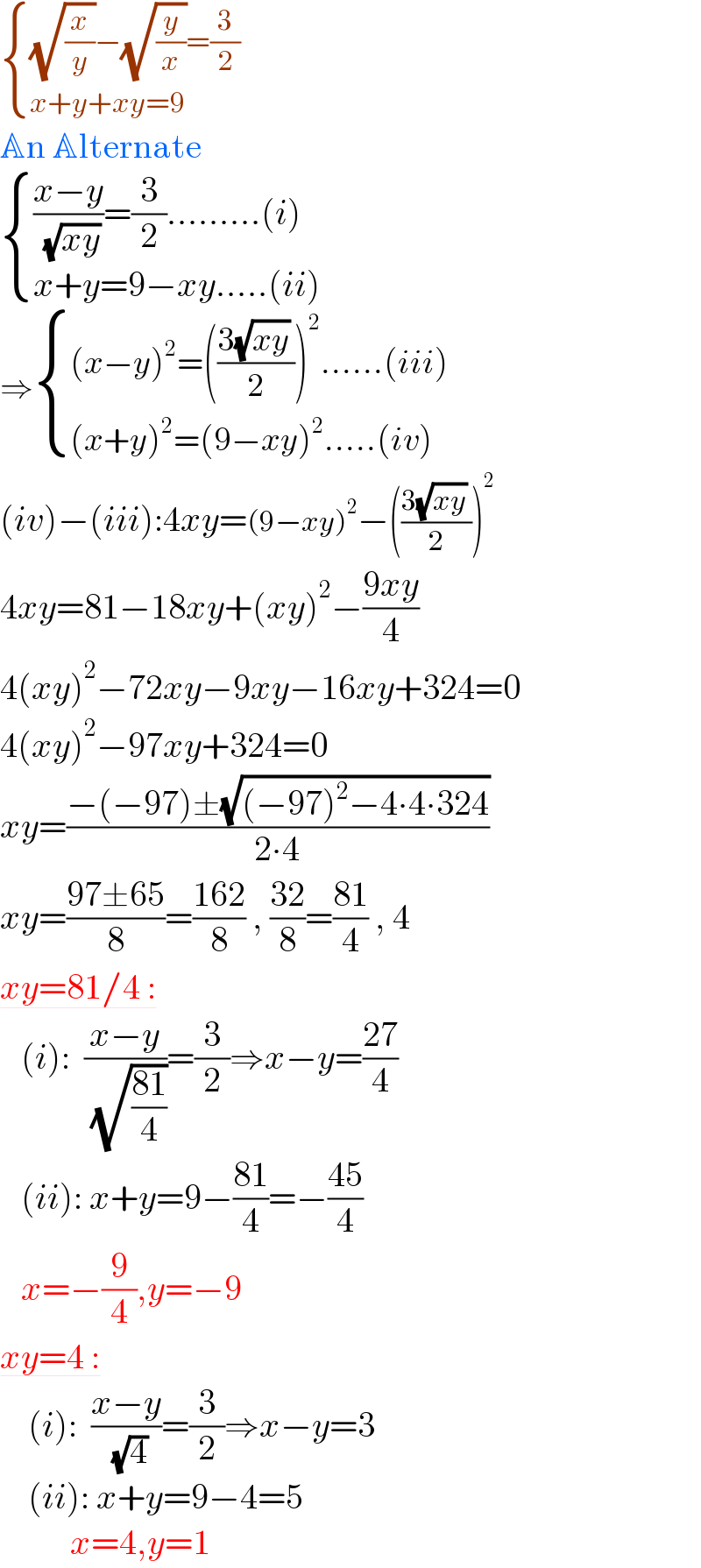
$$\begin{cases}{\sqrt{\frac{{x}}{{y}}}−\sqrt{\frac{{y}}{{x}}}=\frac{\mathrm{3}}{\mathrm{2}}}\\{{x}+{y}+{xy}=\mathrm{9}}\end{cases}\: \\ $$$$\mathbb{A}\mathrm{n}\:\mathbb{A}\mathrm{lternate} \\ $$$$\begin{cases}{\frac{{x}−{y}}{\:\sqrt{{xy}}}=\frac{\mathrm{3}}{\mathrm{2}}.........\left({i}\right)}\\{{x}+{y}=\mathrm{9}−{xy}.....\left({ii}\right)}\end{cases}\: \\ $$$$\Rightarrow\begin{cases}{\left({x}−{y}\right)^{\mathrm{2}} =\left(\frac{\mathrm{3}\sqrt{{xy}}\:}{\mathrm{2}}\right)^{\mathrm{2}} ......\left({iii}\right)}\\{\left({x}+{y}\right)^{\mathrm{2}} =\left(\mathrm{9}−{xy}\right)^{\mathrm{2}} .....\left({iv}\right)}\end{cases} \\ $$$$\left({iv}\right)−\left({iii}\right):\mathrm{4}{xy}=\left(\mathrm{9}−{xy}\right)^{\mathrm{2}} −\left(\frac{\mathrm{3}\sqrt{{xy}}\:}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{4}{xy}=\mathrm{81}−\mathrm{18}{xy}+\left({xy}\right)^{\mathrm{2}} −\frac{\mathrm{9}{xy}}{\mathrm{4}} \\ $$$$\mathrm{4}\left({xy}\right)^{\mathrm{2}} −\mathrm{72}{xy}−\mathrm{9}{xy}−\mathrm{16}{xy}+\mathrm{324}=\mathrm{0} \\ $$$$\mathrm{4}\left({xy}\right)^{\mathrm{2}} −\mathrm{97}{xy}+\mathrm{324}=\mathrm{0} \\ $$$${xy}=\frac{−\left(−\mathrm{97}\right)\pm\sqrt{\left(−\mathrm{97}\right)^{\mathrm{2}} −\mathrm{4}\centerdot\mathrm{4}\centerdot\mathrm{324}}}{\mathrm{2}\centerdot\mathrm{4}} \\ $$$${xy}=\frac{\mathrm{97}\pm\mathrm{65}}{\mathrm{8}}=\frac{\mathrm{162}}{\mathrm{8}}\:,\:\frac{\mathrm{32}}{\mathrm{8}}=\frac{\mathrm{81}}{\mathrm{4}}\:,\:\mathrm{4} \\ $$$$\underline{{xy}=\mathrm{81}/\mathrm{4}\::} \\ $$$$\:\:\:\left({i}\right):\:\:\frac{{x}−{y}}{\:\sqrt{\frac{\mathrm{81}}{\mathrm{4}}}}=\frac{\mathrm{3}}{\mathrm{2}}\Rightarrow{x}−{y}=\frac{\mathrm{27}}{\mathrm{4}} \\ $$$$\:\:\:\left({ii}\right):\:{x}+{y}=\mathrm{9}−\frac{\mathrm{81}}{\mathrm{4}}=−\frac{\mathrm{45}}{\mathrm{4}} \\ $$$$\:\:\:{x}=−\frac{\mathrm{9}}{\mathrm{4}},{y}=−\mathrm{9} \\ $$$$\underline{{xy}=\mathrm{4}\::} \\ $$$$\:\:\:\:\left({i}\right):\:\:\frac{{x}−{y}}{\:\sqrt{\mathrm{4}}}=\frac{\mathrm{3}}{\mathrm{2}}\Rightarrow{x}−{y}=\mathrm{3} \\ $$$$\:\:\:\:\left({ii}\right):\:{x}+{y}=\mathrm{9}−\mathrm{4}=\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}=\mathrm{4},{y}=\mathrm{1} \\ $$
