
Question Number 165853 by mathlove last updated on 09/Feb/22
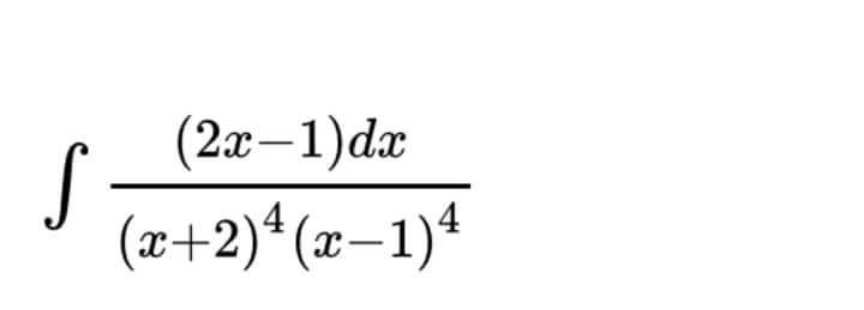
Answered by MJS_new last updated on 09/Feb/22
![∫((2x−1)/((x+2)^4 (x−1)^4 ))dx= [Ostrogradski′s Method] =((40x^5 +100x^4 −140x^3 −310x^2 +278x−49)/(729(x−1)^3 (x+2)^3 ))+((40)/(729))∫(dx/((x−1)(x+2)))= [∫(dx/((x−1)(x+2)))=(1/3)∫((1/(x−1))−(1/(x+2)))dx=(1/3)ln ∣((x−1)/(x+2))∣] ==((40x^5 +100x^4 −140x^3 −310x^2 +278x−49)/(729(x−1)^3 (x+2)^3 ))+((40)/(2187))ln ∣((x−1)/(x+2))∣ +C](Q165856.png)
$$\int\frac{\mathrm{2}{x}−\mathrm{1}}{\left({x}+\mathrm{2}\right)^{\mathrm{4}} \left({x}−\mathrm{1}\right)^{\mathrm{4}} }{dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=\frac{\mathrm{40}{x}^{\mathrm{5}} +\mathrm{100}{x}^{\mathrm{4}} −\mathrm{140}{x}^{\mathrm{3}} −\mathrm{310}{x}^{\mathrm{2}} +\mathrm{278}{x}−\mathrm{49}}{\mathrm{729}\left({x}−\mathrm{1}\right)^{\mathrm{3}} \left({x}+\mathrm{2}\right)^{\mathrm{3}} }+\frac{\mathrm{40}}{\mathrm{729}}\int\frac{{dx}}{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{2}\right)}= \\ $$$$\:\:\:\:\:\left[\int\frac{{dx}}{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{2}\right)}=\frac{\mathrm{1}}{\mathrm{3}}\int\left(\frac{\mathrm{1}}{{x}−\mathrm{1}}−\frac{\mathrm{1}}{{x}+\mathrm{2}}\right){dx}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{2}}\mid\right] \\ $$$$==\frac{\mathrm{40}{x}^{\mathrm{5}} +\mathrm{100}{x}^{\mathrm{4}} −\mathrm{140}{x}^{\mathrm{3}} −\mathrm{310}{x}^{\mathrm{2}} +\mathrm{278}{x}−\mathrm{49}}{\mathrm{729}\left({x}−\mathrm{1}\right)^{\mathrm{3}} \left({x}+\mathrm{2}\right)^{\mathrm{3}} }+\frac{\mathrm{40}}{\mathrm{2187}}\mathrm{ln}\:\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{2}}\mid\:+{C} \\ $$
