Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 165851 by Bagus1003 last updated on 09/Feb/22

2(cos(45))^4 = (1/2) ร— (๐›•/(x ร— 2)) + 1 โˆ’ (2/2) How much the x is?

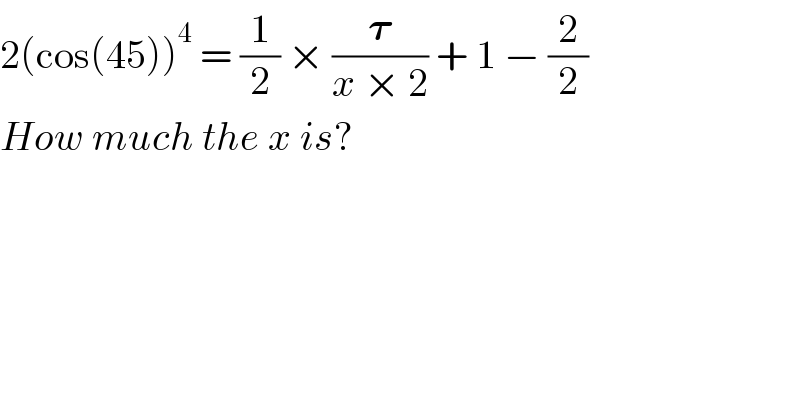
$$\mathrm{2}\left(\mathrm{cos}\left(\mathrm{45}\right)\right)^{\mathrm{4}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\:ร—\:\frac{\boldsymbol{\tau}}{{x}\:ร—\:\mathrm{2}}\:+\:\mathrm{1}\:โˆ’\:\frac{\mathrm{2}}{\mathrm{2}} \\ $$$${How}\:{much}\:{the}\:{x}\:{is}? \\ $$

Answered by MJS_new last updated on 09/Feb/22

2(cos(45))^4 =(1/2)ร—(ฯ„/(xร—2))+1โˆ’(2/2) 2(cos(45))^4 โˆ’1+(2/2) =(1/2)ร—(ฯ„/(xร—2)) (2(cos(45))^4 โˆ’1+(2/2) )รท(1/2)=(ฯ„/(xร—2)) (((2(cos(45))^4 โˆ’1+(2/2) )รท(1/2))/ฯ„)=(1/(xร—2)) xร—2ร—(((2(cos(45))^4 โˆ’1+(2/2) )รท(1/2))/ฯ„)=1 x=(1/(2ร—(((2(cos(45))^4 โˆ’1+(2/2) )รท(1/2))/ฯ„)))

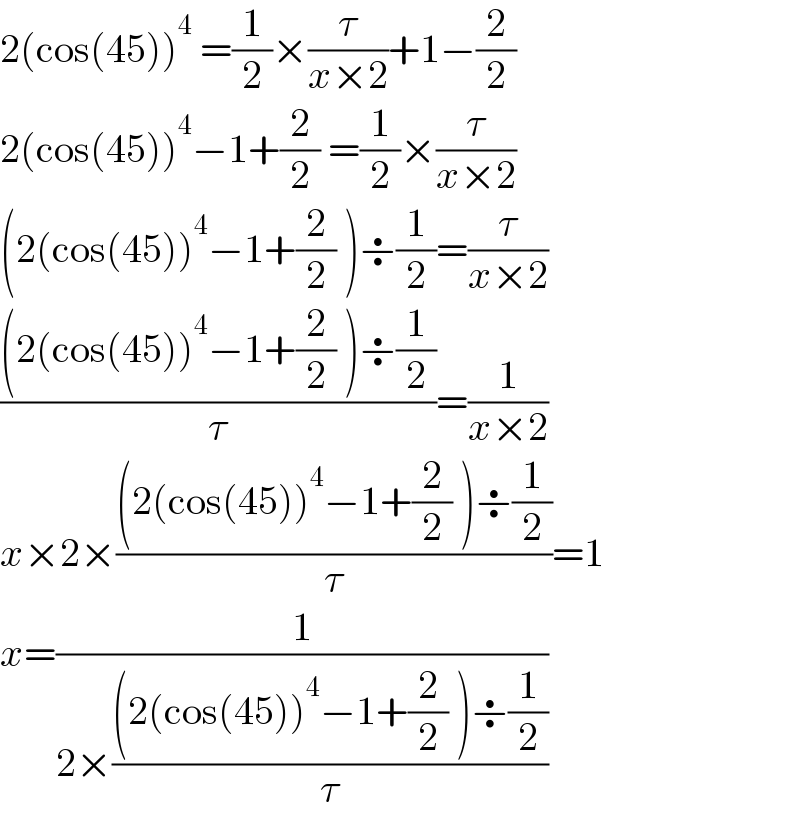
$$\mathrm{2}\left(\mathrm{cos}\left(\mathrm{45}\right)\right)^{\mathrm{4}} \:=\frac{\mathrm{1}}{\mathrm{2}}ร—\frac{\tau}{{x}ร—\mathrm{2}}+\mathrm{1}โˆ’\frac{\mathrm{2}}{\mathrm{2}} \\ $$$$\mathrm{2}\left(\mathrm{cos}\left(\mathrm{45}\right)\right)^{\mathrm{4}} โˆ’\mathrm{1}+\frac{\mathrm{2}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}ร—\frac{\tau}{{x}ร—\mathrm{2}} \\ $$$$\left(\mathrm{2}\left(\mathrm{cos}\left(\mathrm{45}\right)\right)^{\mathrm{4}} โˆ’\mathrm{1}+\frac{\mathrm{2}}{\mathrm{2}}\:\right)\boldsymbol{\div}\frac{\mathrm{1}}{\mathrm{2}}=\frac{\tau}{{x}ร—\mathrm{2}} \\ $$$$\frac{\left(\mathrm{2}\left(\mathrm{cos}\left(\mathrm{45}\right)\right)^{\mathrm{4}} โˆ’\mathrm{1}+\frac{\mathrm{2}}{\mathrm{2}}\:\right)\boldsymbol{\div}\frac{\mathrm{1}}{\mathrm{2}}}{\tau}=\frac{\mathrm{1}}{{x}ร—\mathrm{2}} \\ $$$${x}ร—\mathrm{2}ร—\frac{\left(\mathrm{2}\left(\mathrm{cos}\left(\mathrm{45}\right)\right)^{\mathrm{4}} โˆ’\mathrm{1}+\frac{\mathrm{2}}{\mathrm{2}}\:\right)\boldsymbol{\div}\frac{\mathrm{1}}{\mathrm{2}}}{\tau}=\mathrm{1} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}ร—\frac{\left(\mathrm{2}\left(\mathrm{cos}\left(\mathrm{45}\right)\right)^{\mathrm{4}} โˆ’\mathrm{1}+\frac{\mathrm{2}}{\mathrm{2}}\:\right)\boldsymbol{\div}\frac{\mathrm{1}}{\mathrm{2}}}{\tau}} \\ $$

Answered by Bagus1003 last updated on 09/Feb/22

cos(45)=((โˆš2)/2) (((โˆš2)/2))^2 =(2/4)=(1/2) ((1/2))^2 =(1/4) (((โˆš2)/2))^4 =(1/4) 2ร—(1/4)=(1/2) (1/2)=(1/2)ร—(ฯ„/(xร—2))+1โˆ’(2/2) 0.5=0.5ร—(ฯ„/(xร—2)) 0.5/0.5=1 Substitute them 1=(ฯ„/(xร—2)) ฯ„=2ฯ€ 1=((2ฯ€)/(xร—2)) (xร—2)1=((2ฯ€)/(xร—2))ร—(xร—2) xร—2=2ร—ฯ€ 2/xร—2=2ร—ฯ€/2 2/2=1 The result of x is x=3.14..=ฯ€

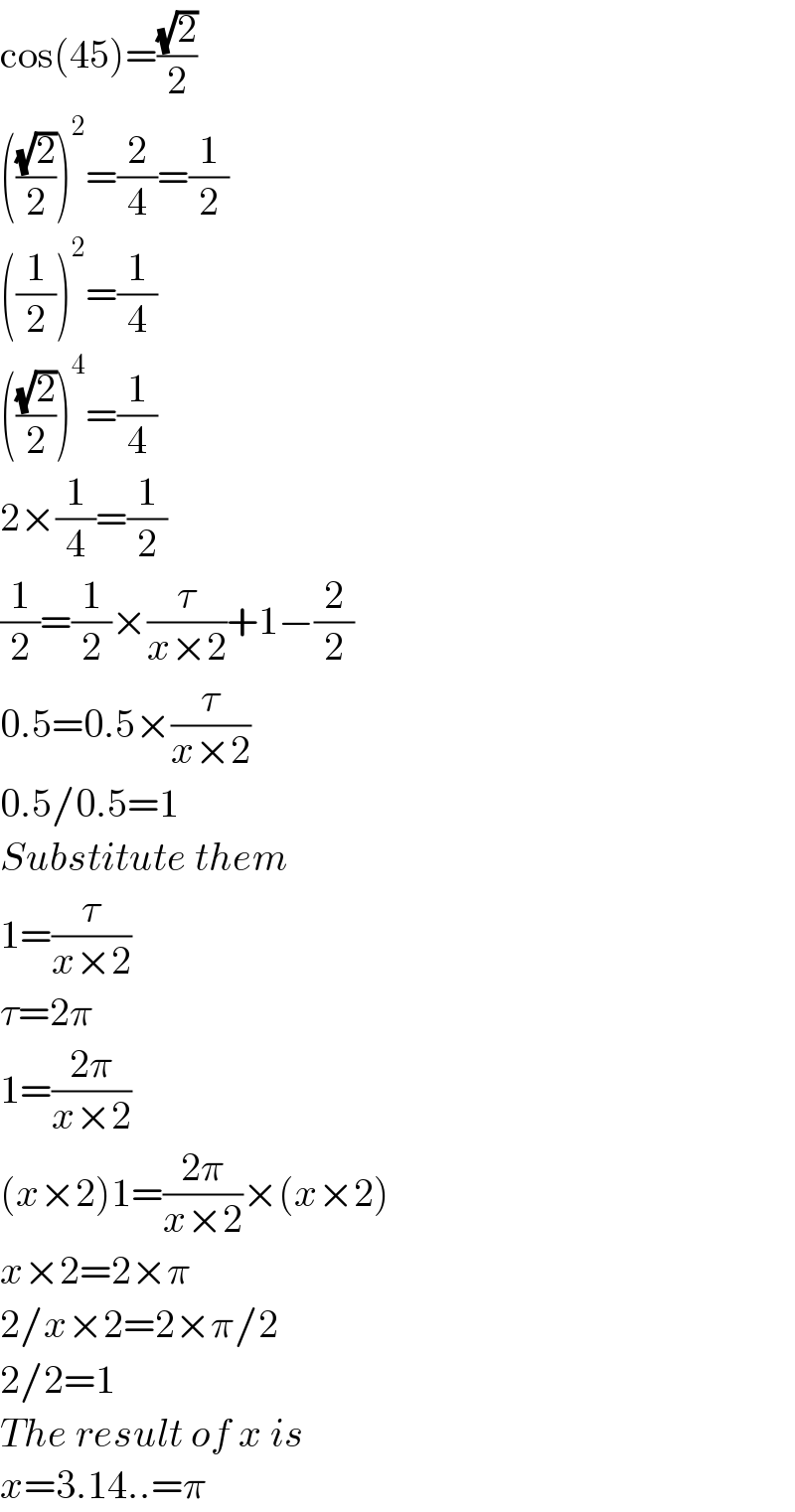
$$\mathrm{cos}\left(\mathrm{45}\right)=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{2}ร—\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}ร—\frac{\tau}{{x}ร—\mathrm{2}}+\mathrm{1}โˆ’\frac{\mathrm{2}}{\mathrm{2}} \\ $$$$\mathrm{0}.\mathrm{5}=\mathrm{0}.\mathrm{5}ร—\frac{\tau}{{x}ร—\mathrm{2}} \\ $$$$\mathrm{0}.\mathrm{5}/\mathrm{0}.\mathrm{5}=\mathrm{1} \\ $$$${Substitute}\:{them} \\ $$$$\mathrm{1}=\frac{\tau}{{x}ร—\mathrm{2}} \\ $$$$\tau=\mathrm{2}\pi \\ $$$$\mathrm{1}=\frac{\mathrm{2}\pi}{{x}ร—\mathrm{2}} \\ $$$$\left({x}ร—\mathrm{2}\right)\mathrm{1}=\frac{\mathrm{2}\pi}{{x}ร—\mathrm{2}}ร—\left({x}ร—\mathrm{2}\right) \\ $$$${x}ร—\mathrm{2}=\mathrm{2}ร—\pi \\ $$$$\mathrm{2}/{x}ร—\mathrm{2}=\mathrm{2}ร—\pi/\mathrm{2} \\ $$$$\mathrm{2}/\mathrm{2}=\mathrm{1} \\ $$$${The}\:{result}\:{of}\:{x}\:{is} \\ $$$${x}=\mathrm{3}.\mathrm{14}..=\pi \\ $$

Commented by MJS_new last updated on 09/Feb/22

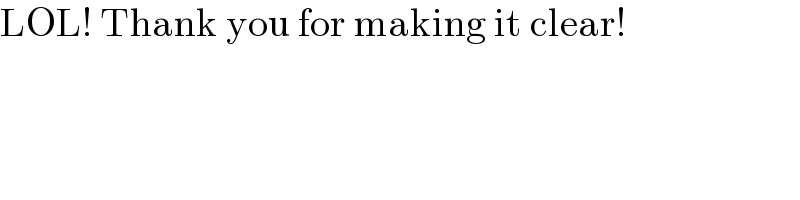
LOL! Thank you for making it clear!

$$\mathrm{LOL}!\:\mathrm{Thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{making}\:\mathrm{it}\:\mathrm{clear}! \\ $$

Commented by Bagus1003 last updated on 09/Feb/22

No problem dude

$${No}\:{problem}\:{dude} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com