
Question Number 165830 by HongKing last updated on 09/Feb/22
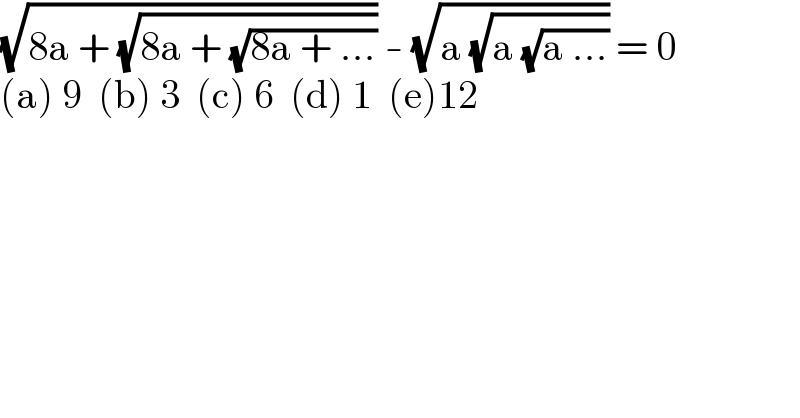
$$\sqrt{\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:...}}}\:-\:\sqrt{\mathrm{a}\:\sqrt{\mathrm{a}\:\sqrt{\mathrm{a}\:...}}}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{a}\right)\:\mathrm{9}\:\:\left(\mathrm{b}\right)\:\mathrm{3}\:\:\left(\mathrm{c}\right)\:\mathrm{6}\:\:\left(\mathrm{d}\right)\:\mathrm{1}\:\:\left(\mathrm{e}\right)\mathrm{12} \\ $$
Answered by Rasheed.Sindhi last updated on 09/Feb/22
![(√(8a + (√(8a + (√(8a + ...)))))) - (√(a (√(a (√(a ...)))))) = 0 (√(8a + (√(8a + (√(8a + ...)))))) = (√(a (√(a (√(a ...)))))) = b(say) 8a + (√(8a + (√(8a + ...)))) = a (√(a (√(a ...)))) 8a+b=ab 8a=b(a−1) b=((8a)/(a−1))............(i) Again, (√(8a + (√(8a + (√(8a + ...)))))) = (√(a (√(a (√(a ...)))))) 8a + (√(8a + (√(8a + ...)))) = a (√(a (√(a ...)))) (√(8a + (√(8a + ...)))) =ab−8a 8a + (√(8a + ...)) =(ab−8a)^2 (√(8a + ...)) =(ab−8a)^2 −8a b =(ab−8a)^2 −8a ((8a)/(a−1))=(a(((8a)/(a−1)))−8a)^2 −8a [∵ b=((8a)/(a−1)) from (i)] ((8a)/(a−1))=(((8a^2 −8a^2 +8a)/(a−1)))^2 −8a ((8a)/(a−1))=(((8a)/(a−1)))^2 −8a 8a(a−1)=64a^2 −8a(a−1)^2 64a^2 =8a(a−1)+8a(a−1)^2 =8a(a−1)(1+a−1) =8a^2 (a−1) a−1=8 a=9](Q165843.png)
$$\sqrt{\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:...}}}\:-\:\sqrt{\mathrm{a}\:\sqrt{\mathrm{a}\:\sqrt{\mathrm{a}\:...}}}\:=\:\mathrm{0} \\ $$$$\sqrt{\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:...}}}\:=\:\sqrt{\mathrm{a}\:\sqrt{\mathrm{a}\:\sqrt{\mathrm{a}\:...}}}\:=\:\mathrm{b}\left(\mathrm{say}\right) \\ $$$$\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:...}}\:=\:\mathrm{a}\:\sqrt{\mathrm{a}\:\sqrt{\mathrm{a}\:...}}\: \\ $$$$\mathrm{8a}+\mathrm{b}=\mathrm{ab} \\ $$$$\mathrm{8a}=\mathrm{b}\left(\mathrm{a}−\mathrm{1}\right) \\ $$$$\mathrm{b}=\frac{\mathrm{8a}}{\mathrm{a}−\mathrm{1}}............\left(\mathrm{i}\right) \\ $$$$\mathrm{Again}, \\ $$$$\sqrt{\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:...}}}\:=\:\sqrt{\mathrm{a}\:\sqrt{\mathrm{a}\:\sqrt{\mathrm{a}\:...}}}\: \\ $$$$\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:...}}\:=\:\mathrm{a}\:\sqrt{\mathrm{a}\:\sqrt{\mathrm{a}\:...}}\: \\ $$$$\:\sqrt{\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:...}}\:=\mathrm{ab}−\mathrm{8a} \\ $$$$\:\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:...}\:=\left(\mathrm{ab}−\mathrm{8a}\right)^{\mathrm{2}} \\ $$$$\:\:\sqrt{\mathrm{8a}\:+\:...}\:=\left(\mathrm{ab}−\mathrm{8a}\right)^{\mathrm{2}} −\mathrm{8a} \\ $$$$\:\:\mathrm{b}\:=\left(\mathrm{ab}−\mathrm{8a}\right)^{\mathrm{2}} −\mathrm{8a} \\ $$$$\frac{\mathrm{8a}}{\mathrm{a}−\mathrm{1}}=\left(\mathrm{a}\left(\frac{\mathrm{8a}}{\mathrm{a}−\mathrm{1}}\right)−\mathrm{8a}\right)^{\mathrm{2}} −\mathrm{8a}\:\left[\because\:\mathrm{b}=\frac{\mathrm{8a}}{\mathrm{a}−\mathrm{1}}\:\mathrm{from}\:\left(\mathrm{i}\right)\right] \\ $$$$\frac{\mathrm{8a}}{\mathrm{a}−\mathrm{1}}=\left(\frac{\mathrm{8a}^{\mathrm{2}} −\mathrm{8a}^{\mathrm{2}} +\mathrm{8a}}{\mathrm{a}−\mathrm{1}}\right)^{\mathrm{2}} −\mathrm{8a} \\ $$$$\frac{\mathrm{8a}}{\mathrm{a}−\mathrm{1}}=\left(\frac{\mathrm{8a}}{\mathrm{a}−\mathrm{1}}\right)^{\mathrm{2}} −\mathrm{8a} \\ $$$$\mathrm{8a}\left(\mathrm{a}−\mathrm{1}\right)=\mathrm{64a}^{\mathrm{2}} −\mathrm{8a}\left(\mathrm{a}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{64a}^{\mathrm{2}} =\mathrm{8a}\left(\mathrm{a}−\mathrm{1}\right)+\mathrm{8a}\left(\mathrm{a}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{8a}\left(\mathrm{a}−\mathrm{1}\right)\left(\mathrm{1}+\mathrm{a}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{8a}^{\mathrm{2}} \left(\mathrm{a}−\mathrm{1}\right) \\ $$$$\mathrm{a}−\mathrm{1}=\mathrm{8} \\ $$$$\mathrm{a}=\mathrm{9} \\ $$
Commented by Tawa11 last updated on 10/Feb/22

$$\mathrm{Weldone}\:\mathrm{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 10/Feb/22

$$\mathbb{T}\mathrm{han}\Bbbk\mathrm{s}\:\mathrm{miss}! \\ $$
Answered by naka3546 last updated on 09/Feb/22
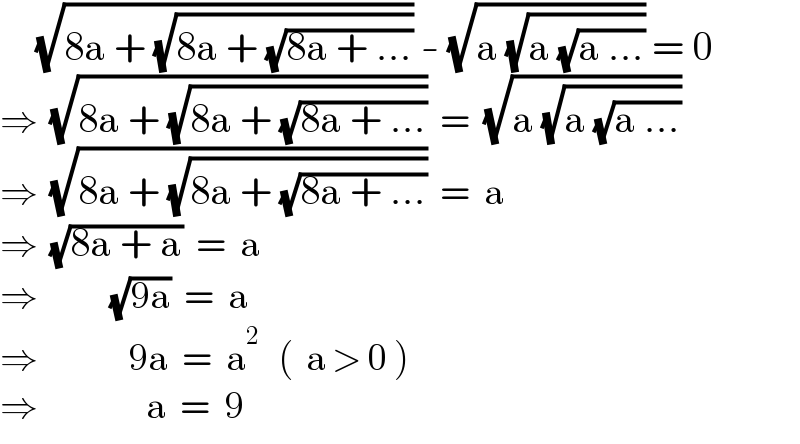
$$\:\:\:\:\:\:\sqrt{\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:...}}}\:-\:\sqrt{\mathrm{a}\:\sqrt{\mathrm{a}\:\sqrt{\mathrm{a}\:...}}}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\sqrt{\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:...}}}\:\:=\:\:\sqrt{\mathrm{a}\:\sqrt{\mathrm{a}\:\sqrt{\mathrm{a}\:...}}}\: \\ $$$$\Rightarrow\:\:\sqrt{\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:\sqrt{\mathrm{8a}\:+\:...}}}\:\:=\:\:\mathrm{a}\: \\ $$$$\Rightarrow\:\:\sqrt{\mathrm{8a}\:+\:\mathrm{a}}\:\:=\:\:\mathrm{a}\: \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{\mathrm{9a}}\:\:=\:\:\mathrm{a}\: \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{9a}\:\:=\:\:\mathrm{a}^{\mathrm{2}} \:\:\:\left(\:\:\mathrm{a}\:>\:\mathrm{0}\:\right) \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{a}\:\:=\:\:\mathrm{9} \\ $$
Commented by Tawa11 last updated on 10/Feb/22

$$\mathrm{Weldone}\:\mathrm{sir} \\ $$
