
Question Number 165742 by amin96 last updated on 07/Feb/22
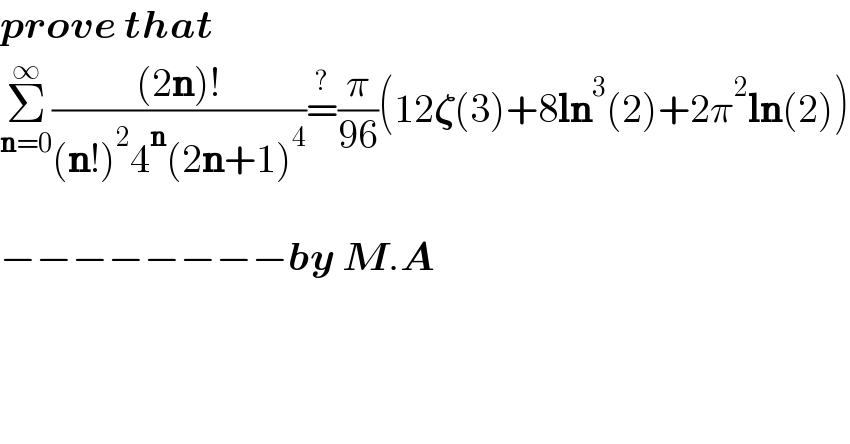
$$\boldsymbol{{prove}}\:\boldsymbol{{that}} \\ $$$$\underset{\boldsymbol{\mathrm{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{2}\boldsymbol{\mathrm{n}}\right)!}{\left(\boldsymbol{\mathrm{n}}!\right)^{\mathrm{2}} \mathrm{4}^{\boldsymbol{\mathrm{n}}} \left(\mathrm{2}\boldsymbol{\mathrm{n}}+\mathrm{1}\right)^{\mathrm{4}} }\overset{?} {=}\frac{\pi}{\mathrm{96}}\left(\mathrm{12}\boldsymbol{\zeta}\left(\mathrm{3}\right)+\mathrm{8}\boldsymbol{\mathrm{ln}}^{\mathrm{3}} \left(\mathrm{2}\right)+\mathrm{2}\pi^{\mathrm{2}} \boldsymbol{\mathrm{ln}}\left(\mathrm{2}\right)\right) \\ $$$$ \\ $$$$−−−−−−−−\boldsymbol{{by}}\:\boldsymbol{{M}}.\boldsymbol{{A}} \\ $$
