
Question Number 165725 by mathocean1 last updated on 06/Feb/22
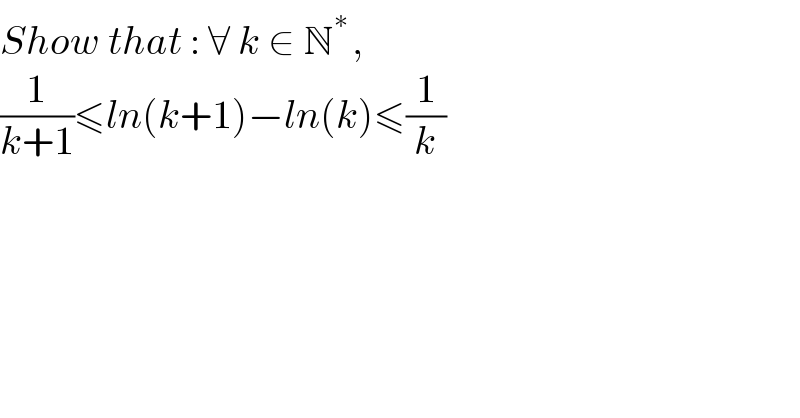
$${Show}\:{that}\::\:\forall\:{k}\:\in\:\mathbb{N}^{\ast\:} ,\: \\ $$$$\frac{\mathrm{1}}{{k}+\mathrm{1}}\leqslant{ln}\left({k}+\mathrm{1}\right)−{ln}\left({k}\right)\leqslant\frac{\mathrm{1}}{{k}} \\ $$
Answered by TheSupreme last updated on 07/Feb/22
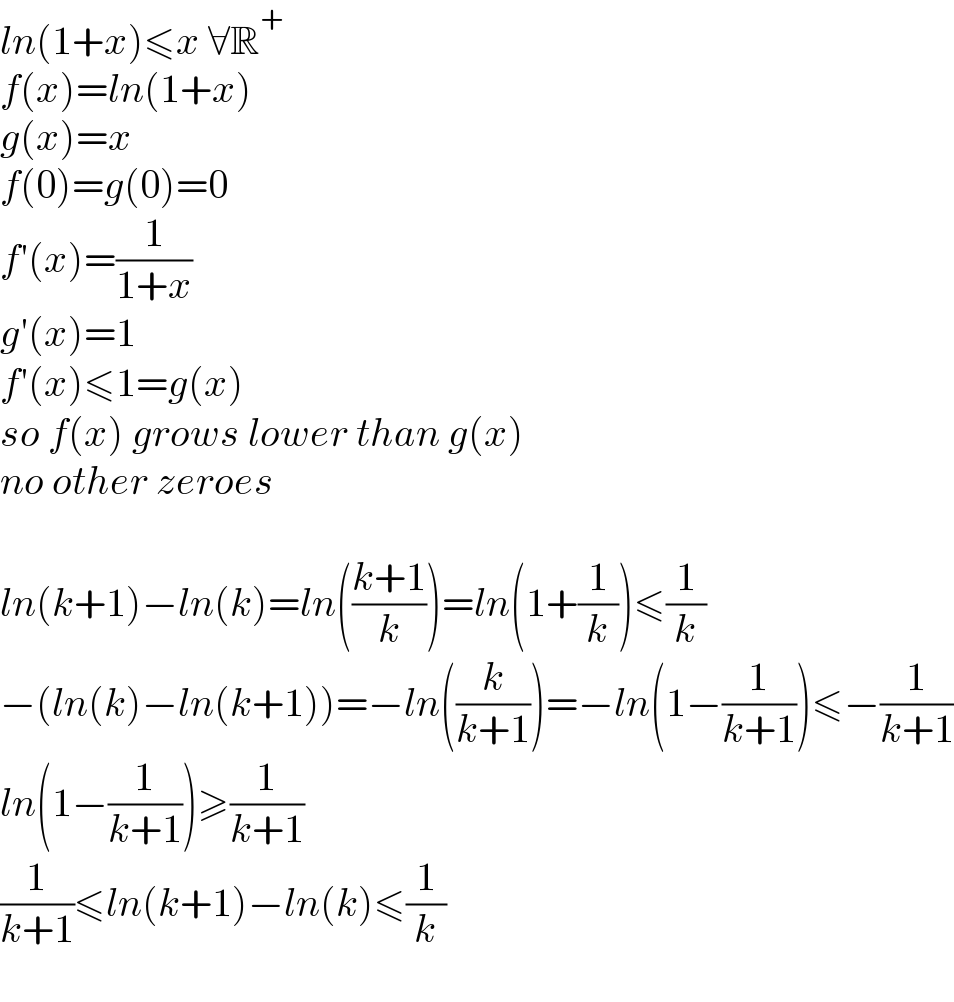
$${ln}\left(\mathrm{1}+{x}\right)\leqslant{x}\:\forall\mathbb{R}^{+} \\ $$$${f}\left({x}\right)={ln}\left(\mathrm{1}+{x}\right) \\ $$$${g}\left({x}\right)={x} \\ $$$${f}\left(\mathrm{0}\right)={g}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${f}'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}+{x}} \\ $$$${g}'\left({x}\right)=\mathrm{1} \\ $$$${f}'\left({x}\right)\leqslant\mathrm{1}={g}\left({x}\right) \\ $$$${so}\:{f}\left({x}\right)\:{grows}\:{lower}\:{than}\:{g}\left({x}\right) \\ $$$${no}\:{other}\:{zeroes}\: \\ $$$$ \\ $$$${ln}\left({k}+\mathrm{1}\right)−{ln}\left({k}\right)={ln}\left(\frac{{k}+\mathrm{1}}{{k}}\right)={ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{k}}\right)\leqslant\frac{\mathrm{1}}{{k}} \\ $$$$−\left({ln}\left({k}\right)−{ln}\left({k}+\mathrm{1}\right)\right)=−{ln}\left(\frac{{k}}{{k}+\mathrm{1}}\right)=−{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{k}+\mathrm{1}}\right)\leqslant−\frac{\mathrm{1}}{{k}+\mathrm{1}} \\ $$$${ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{k}+\mathrm{1}}\right)\geqslant\frac{\mathrm{1}}{{k}+\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{{k}+\mathrm{1}}\leqslant{ln}\left({k}+\mathrm{1}\right)−{ln}\left({k}\right)\leqslant\frac{\mathrm{1}}{{k}} \\ $$$$ \\ $$
