
Question Number 165687 by mnjuly1970 last updated on 06/Feb/22
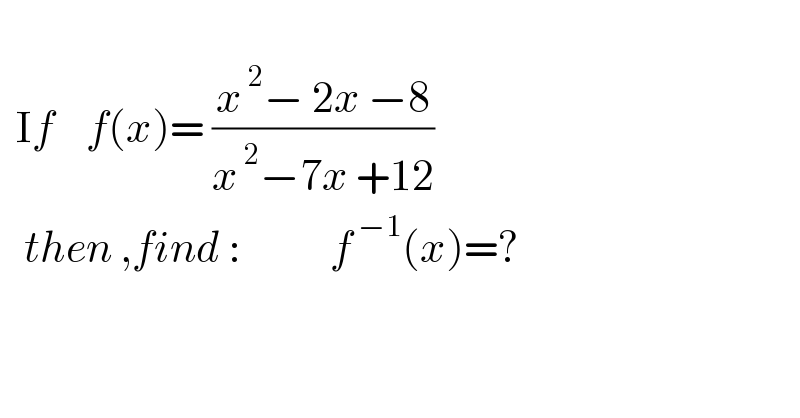
$$ \\ $$$$\:\:\mathrm{I}{f}\:\:\:\:{f}\left({x}\right)=\:\frac{{x}^{\:\mathrm{2}} −\:\mathrm{2}{x}\:−\mathrm{8}}{{x}^{\:\mathrm{2}} −\mathrm{7}{x}\:+\mathrm{12}} \\ $$$$\:\:\:{then}\:,{find}\::\:\:\:\:\:\:\:\:\:\:\:{f}^{\:−\mathrm{1}} \left({x}\right)=? \\ $$$$ \\ $$
Answered by TheSupreme last updated on 07/Feb/22
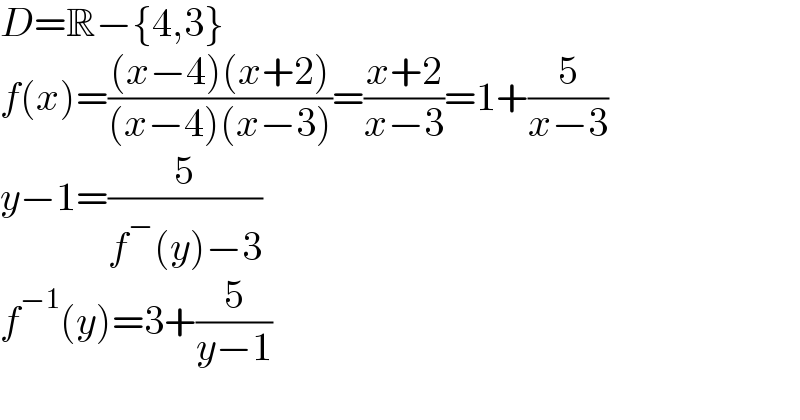
$${D}=\mathbb{R}−\left\{\mathrm{4},\mathrm{3}\right\} \\ $$$${f}\left({x}\right)=\frac{\left({x}−\mathrm{4}\right)\left({x}+\mathrm{2}\right)}{\left({x}−\mathrm{4}\right)\left({x}−\mathrm{3}\right)}=\frac{{x}+\mathrm{2}}{{x}−\mathrm{3}}=\mathrm{1}+\frac{\mathrm{5}}{{x}−\mathrm{3}} \\ $$$${y}−\mathrm{1}=\frac{\mathrm{5}}{{f}^{−} \left({y}\right)−\mathrm{3}} \\ $$$${f}^{−\mathrm{1}} \left({y}\right)=\mathrm{3}+\frac{\mathrm{5}}{{y}−\mathrm{1}} \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 06/Feb/22
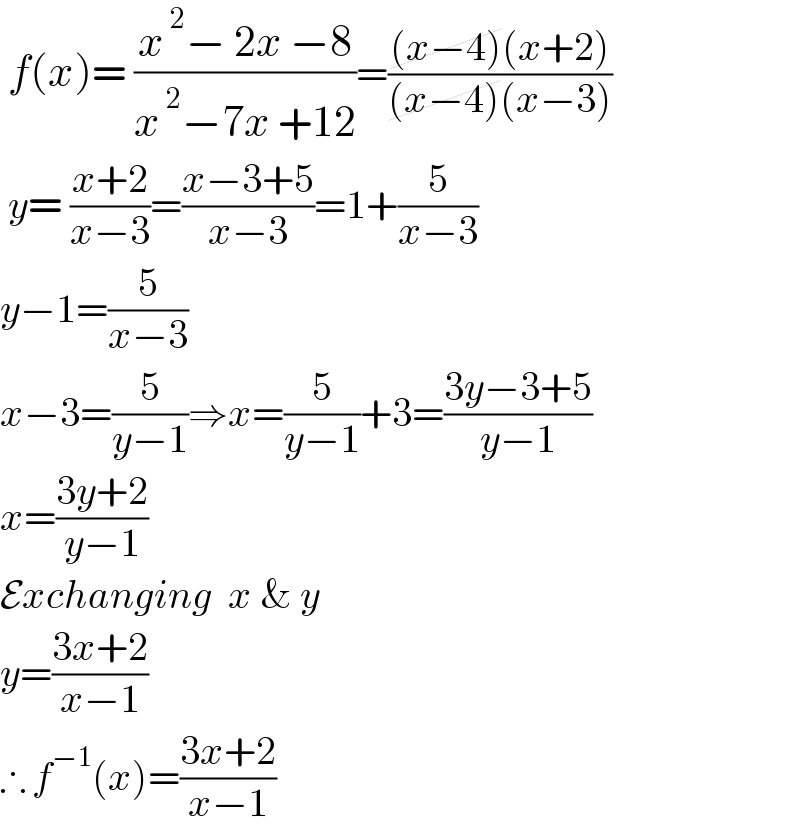
$$\:{f}\left({x}\right)=\:\frac{{x}^{\:\mathrm{2}} −\:\mathrm{2}{x}\:−\mathrm{8}}{{x}^{\:\mathrm{2}} −\mathrm{7}{x}\:+\mathrm{12}}=\frac{\cancel{\left({x}−\mathrm{4}\right)}\left({x}+\mathrm{2}\right)}{\cancel{\left({x}−\mathrm{4}\right)}\left({x}−\mathrm{3}\right)} \\ $$$$\:{y}=\:\frac{{x}+\mathrm{2}}{{x}−\mathrm{3}}=\frac{{x}−\mathrm{3}+\mathrm{5}}{{x}−\mathrm{3}}=\mathrm{1}+\frac{\mathrm{5}}{{x}−\mathrm{3}} \\ $$$${y}−\mathrm{1}=\frac{\mathrm{5}}{{x}−\mathrm{3}} \\ $$$${x}−\mathrm{3}=\frac{\mathrm{5}}{{y}−\mathrm{1}}\Rightarrow{x}=\frac{\mathrm{5}}{{y}−\mathrm{1}}+\mathrm{3}=\frac{\mathrm{3}{y}−\mathrm{3}+\mathrm{5}}{{y}−\mathrm{1}} \\ $$$${x}=\frac{\mathrm{3}{y}+\mathrm{2}}{{y}−\mathrm{1}} \\ $$$$\mathcal{E}{xchanging}\:\:{x}\:\&\:{y} \\ $$$${y}=\frac{\mathrm{3}{x}+\mathrm{2}}{{x}−\mathrm{1}} \\ $$$$\therefore\:{f}^{−\mathrm{1}} \left({x}\right)=\frac{\mathrm{3}{x}+\mathrm{2}}{{x}−\mathrm{1}} \\ $$
