
Question Number 165685 by daus last updated on 06/Feb/22
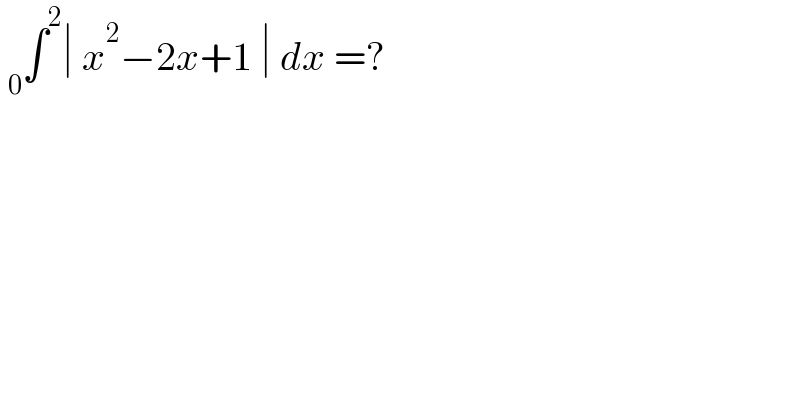
$$\:_{\mathrm{0}} \int^{\mathrm{2}} \mid\:{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\:\mid\:{dx}\:=?\: \\ $$
Answered by TheSupreme last updated on 07/Feb/22
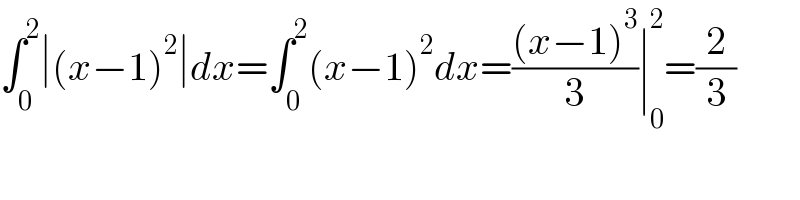
$$\int_{\mathrm{0}} ^{\mathrm{2}} \mid\left({x}−\mathrm{1}\right)^{\mathrm{2}} \mid{dx}=\int_{\mathrm{0}} ^{\mathrm{2}} \left({x}−\mathrm{1}\right)^{\mathrm{2}} {dx}=\frac{\left({x}−\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{3}}\mid_{\mathrm{0}} ^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by mr W last updated on 06/Feb/22

$${wrong}! \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \neq\int_{\mathrm{0}} ^{\mathrm{1}} \\ $$
Answered by alephzero last updated on 06/Feb/22
![∫_0 ^2 ∣x^2 −2x+1∣ dx = = ∫_0 ^2 ∣(x−1)^2 ∣ dx = = ∫_0 ^2 (x−1)^2 dx = = ∫_0 ^2 x^2 −2x+1 dx = = [∫x^2 dx−∫2xdx+∫dx]_0 ^2 = = [(x^3 /3)−((2x^2 )/2)+x]_0 ^2 = = (8/3)−(8/2)+2 = ((16−24)/6)+2 = −(8/6)+ +2 = −(4/3)+2 = 2−(4/3) = ((6−4)/3) = = (2/3)](Q165707.png)
$$\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\mid{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\mid\:{dx}\:= \\ $$$$=\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\mid\left({x}−\mathrm{1}\right)^{\mathrm{2}} \mid\:{dx}\:= \\ $$$$=\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:{dx}\:=\: \\ $$$$=\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\:{dx}\:= \\ $$$$=\:\left[\int{x}^{\mathrm{2}} {dx}−\int\mathrm{2}{xdx}+\int{dx}\right]_{\mathrm{0}} ^{\mathrm{2}} \:= \\ $$$$=\:\left[\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{2}}+{x}\right]_{\mathrm{0}} ^{\mathrm{2}} \:= \\ $$$$=\:\frac{\mathrm{8}}{\mathrm{3}}−\frac{\mathrm{8}}{\mathrm{2}}+\mathrm{2}\:=\:\frac{\mathrm{16}−\mathrm{24}}{\mathrm{6}}+\mathrm{2}\:=\:−\frac{\mathrm{8}}{\mathrm{6}}+ \\ $$$$+\mathrm{2}\:=\:−\frac{\mathrm{4}}{\mathrm{3}}+\mathrm{2}\:=\:\mathrm{2}−\frac{\mathrm{4}}{\mathrm{3}}\:=\:\frac{\mathrm{6}−\mathrm{4}}{\mathrm{3}}\:= \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$
